- Published on
The Blockchain Scaling Dilemma
- Authors

- Name
- Carter Jack Feldman
- @cmpeq
Over the past year, a massive effort has been put into scaling blockchains. With the emergence of Layer 2s, rollups, sharded blockchains and the like, it may seem like we are on the cusp of solving the blockchain scaling dilemma. In this post, we will explore the previous approaches to blockchain scaling and the problems which thus far have prevented the creation of a truly scalable blockchain.
The Traditional Model
Traditional blockchains are have serial state models. By "serial state model," we specifically mean a state model where in each transaction within a given block can theoretically read from or write to any state slot. In practice, this means that we need to sequence our transactions and execute them one at a time. This has the advantage of making the state topology simple, at the cost of scalability.
For example, consider a token contract on a typical blockchain. In the case of an ERC20 token, the smart contract stores the token balance of each user:
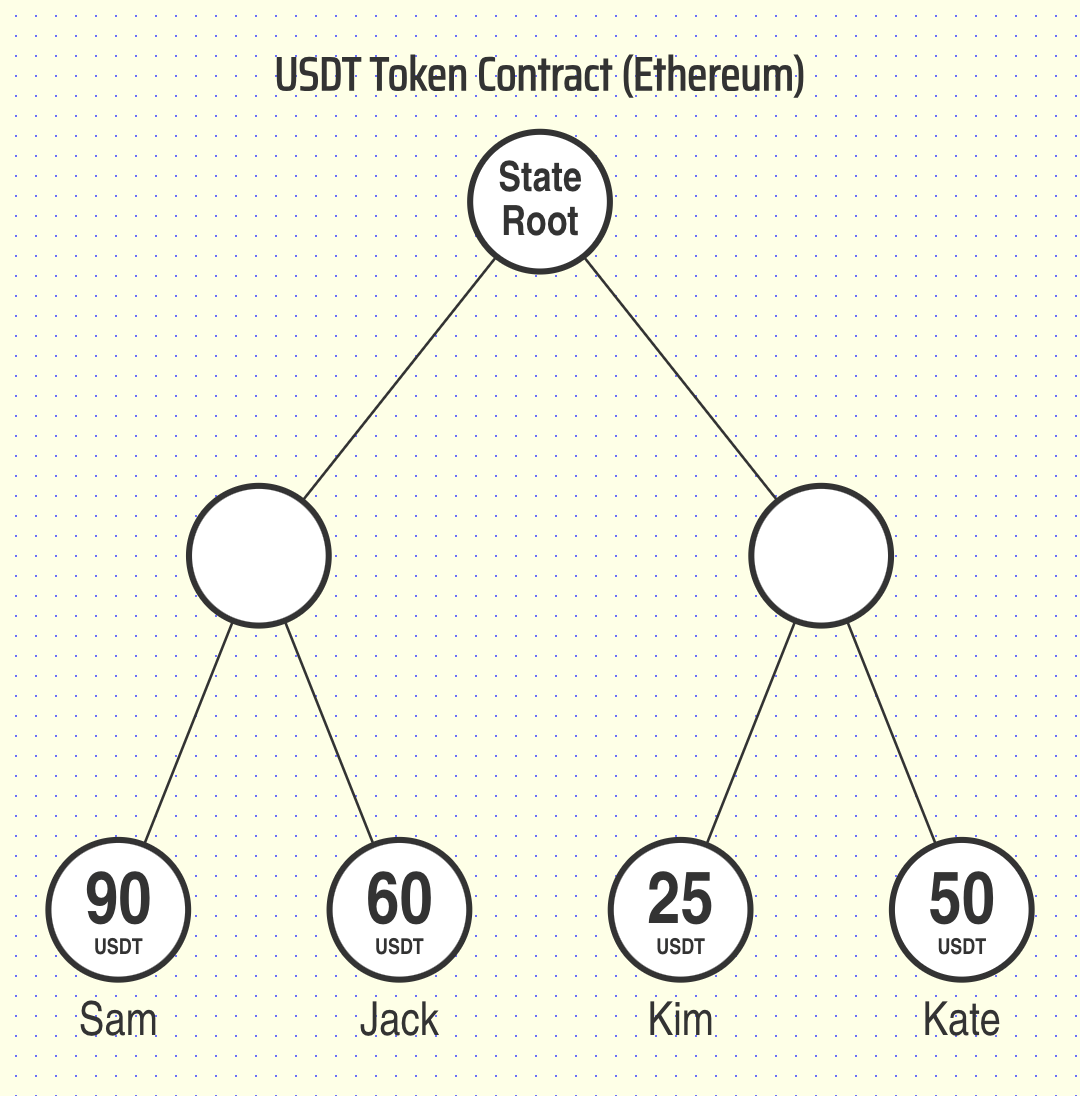
In addition to storing the balance of each user on chain, the ERC20 token contract also exposes a transfer function which allows a user to send funds to another user:
contract ERC20
{
// Modified for brevity from https://github.com/OpenZeppelin/openzeppelin-contracts/blob/master/contracts/token/ERC20/ERC20.sol#L244
...
// store a balance for each user `account`
mapping(address account => uint256) private _balances;
...
function transfer(address from, address to, uint256 value) {
// read the sender's current token balance
uint256 fromBalance = _balances[from];
// if the sender is trying to send more tokens than they own, revert the transaction
if (fromBalance < value) {
revert ERC20InsufficientBalance(from, fromBalance, value);
}
// set the sender's balance to their previous balance - the amount being sent
_balances[from] = fromBalance - value;
// set the recipient's balance to their previous balance + the amount being sent
_balances[to] += value;
}
}
The Scalability Dilemma
While this way of storing and updating token balances is simple, it forces us to execute transactions one-by-one.
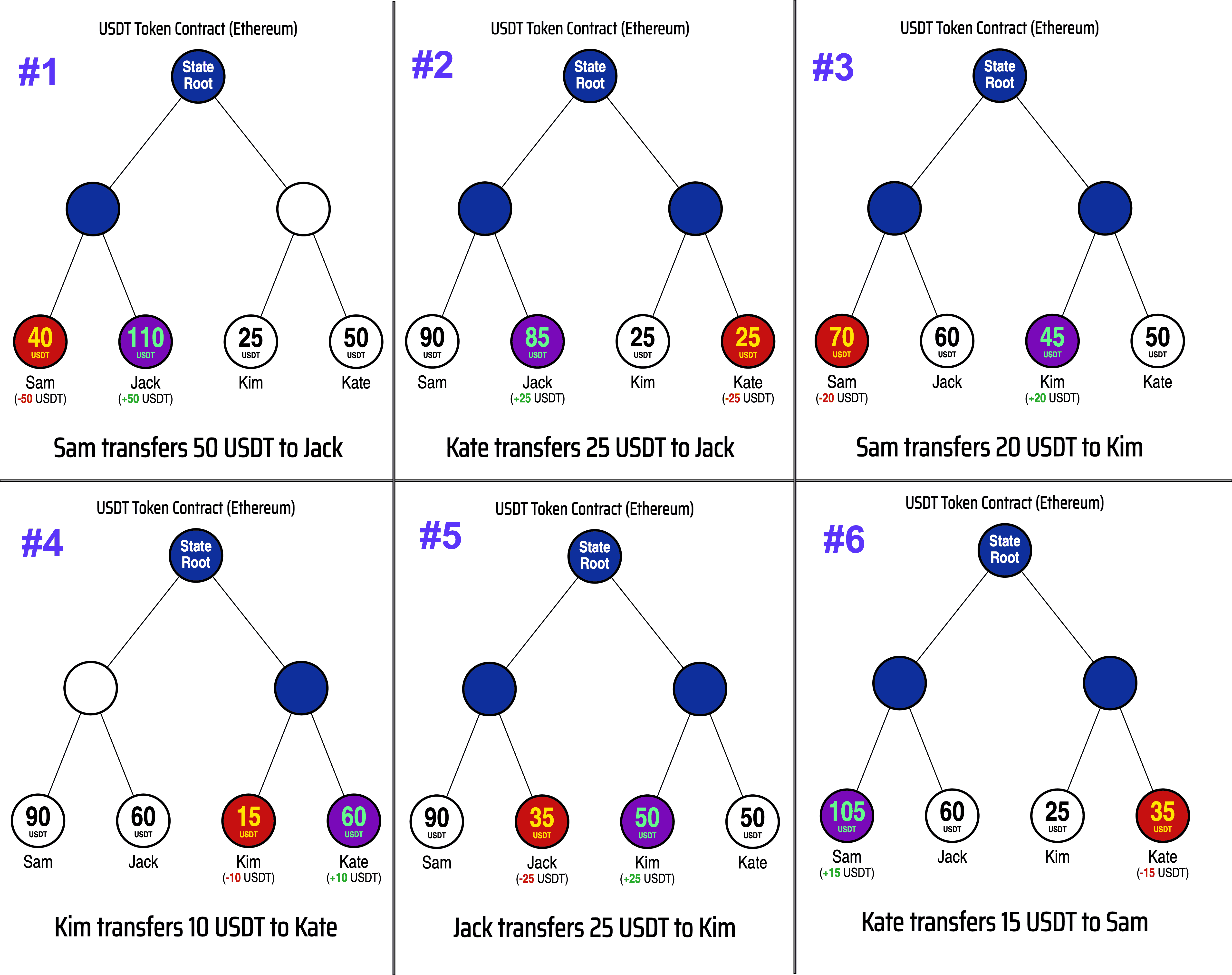
To better understand why this is the case, let's consider the following scenario, where the transactions below are submitted to a block:
Sam transfers $50 to Jack
Kate transfers $25 to Jack
Sam transfers $20 to Kim
Kim transfers $10 to Kate
Jack transfers $25 to Kim
Kate transfers $15 to Sam
If we ran these transactions on a popular blockchain such as Ethereum, the updates would look like the following:
As you can see, when we run the transactions we get the correct answer for the final balances for each user:
| User | Starting Balance | Total Sent | Total Received | Final Balance |
|---|---|---|---|---|
| Bob | $90 | $70 | $15 | $35 |
| Jack | $60 | $25 | $75 | $110 |
| Kim | $25 | $10 | $45 | $60 |
| Kate | $50 | $40 | $10 | $20 |
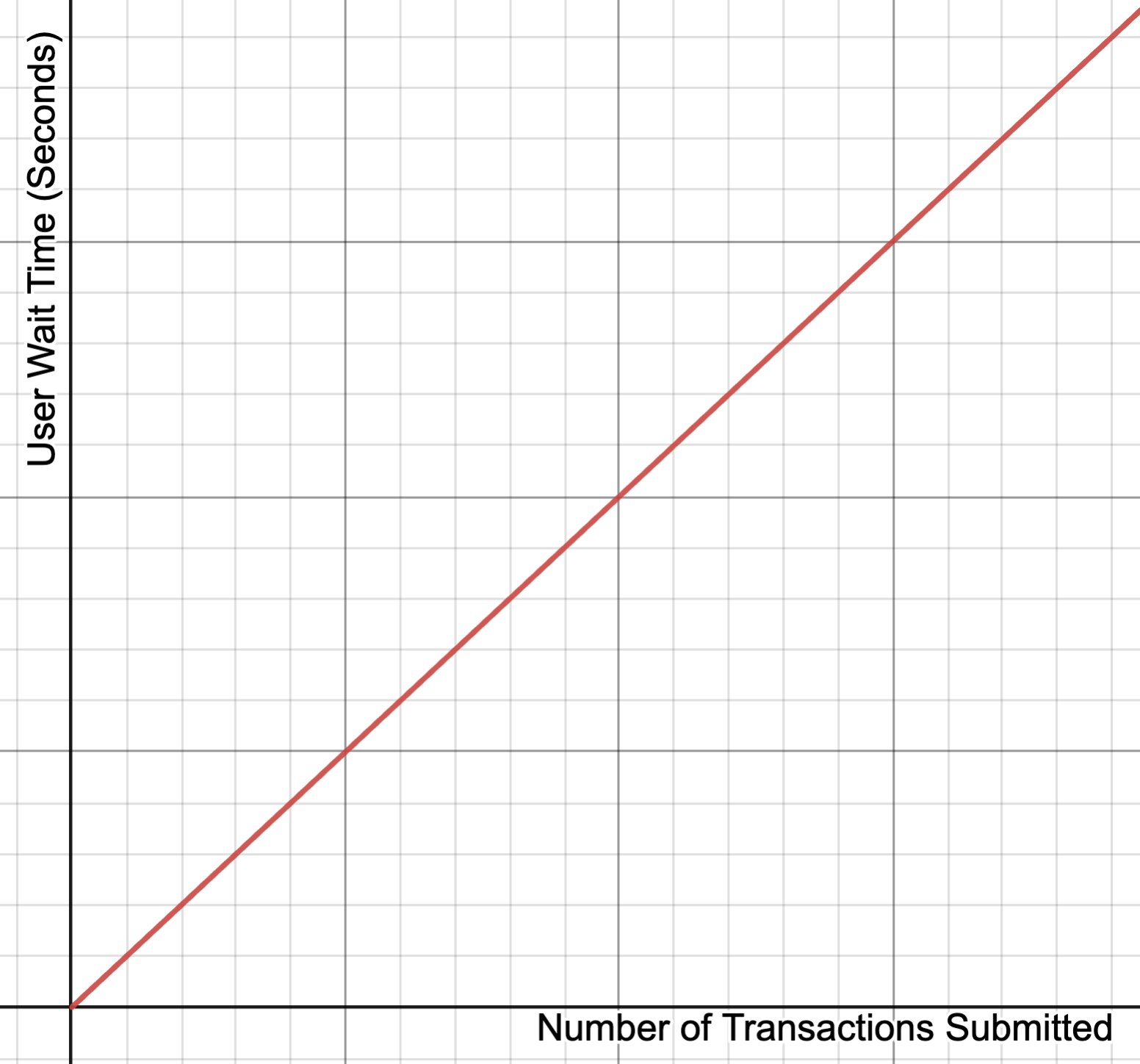
While this approach does work, the time complexity of processing a block with transactions has at least time complexity.
More concretely, if we say that is the average time it takes to execute each transaction in a block with transactions, we have a lower bound for the block time given by:
This is problematic for scaling, since it means the time users have to wait for a transaction to processed increases linearly with blockchain usage:
Parallel Execution?
To get around this linear bottleneck, it may seem tempting to try to run the transactions in parallel (all at the same time) instead of one-by-one.
If we try to run these transactions in parallel, however, we quickly run into a race condition that makes it unclear what the final state of the contract should be. A race condition is a data consistency conflict that occurs when multiple parallel processes try to read and write to the same memory value in parallel, as shown by the results below:
Notice that, when we run the transactions in parallel, each transaction disagrees about what the end users balances should be.
Aren't there Existing Solutions to Blockchain Scalability?
Some blockchains have tried to resolve the race conditions inherent to the serial state model by first running the transactions in parallel, marking which state slots are accessed during a current block, and then falling back to serial execution for those transactions which have conflicting read/writes. Another related approach which tries to solve this issue is sharding, where we isolate reads/writes for a given transaction, ranges will be accessed by a transaction, eliminating the need for fallbacks, at the expense of losing global state (blockchain composability, cross contract calls).
While many blockchains have claimed in marketing materials and in carefully crafted performance demos to be capable of processing 100,000+ transactions per second using these techniques, none are capable of processing the transactions from our simple token example in parallel, and all of them have failed to live up to their marketing TPS promises in practice:
| Blockchain | Claimed "Theoretical" TPS | Actual Max TPS Record* | Percentage of Claim |
|---|---|---|---|
| Sui | 297,000 | 5,414 | 1.82% |
| Aptos | 160,000 | 7,345 | 4.59% |
| Solana | 50,000 | 4,900† / 546 | 9.80%† / 1.09% |
*: Note: TPS record information was collected from reputable, publicly available sources with the longest range of historical data we could find.
†: Note: Solana has reached 5,000 TPS if you include vote transactions (these are not normal user/smart contract transactions), so 546 TPS is a better reflection of the TPS for this comparison.
Marketing vs Reality
You may be asking yourself the question: "Why does the promised theoretical TPS of these chains differ so much from what we actually observe on mainnet?".
The answer is that the sky high TPS figures marketed were benchmarked on a specially prepared set of transactions which could take advantage of the respective blockchain's parallelization strategy executed in ideal conditions, as well as the fact that these benchmark transactions are not representative of the real world transactions people actually want to send on chain.
A good example of this transaction disparity is the fact that neither Sui, Aptos nor Solana are able to parallelize the 6 sample token transfers from the scenario in the previous section.
The inverse correlation between TPS and Security
In addition to fatal not coming close materializing the TPS claims promised in marketing materials, there is a deeper, more sinister flaw with the blockchains which aspire to be massively parallel: an inverse correlation between TPS and security.
To understand why massively parallel blockchains lose security as they scale, let's imagine that someone finally cracked the code and built a massively parallel blockchain which can make uses of thousands of parallel cores running on a distributed compute cluster and can scale to 200k+ TPS with real world (useful) transactions.
While impressive, our hypothetically "perfectly" parallel blockchain begs the question: How much money will it cost to run a full node?
If your full node implementation scales by distributing your transactions in parallel across a datacenter full of servers, only a few big companies with deep pockets will be able to afford to run a full node to actually execute and validate the transactions.
In fact, the more transactions per second you squeeze out of your horizontally scalable blockchain, the more servers you will need and the higher the barrier of entry will be to run a full node. Alternatively, if we instead try to split up the transactions and run bundles of transactions on "partial nodes" with lower requirements, we still find that the number of nodes which process each transaction decreases linearly as our TPS increases.
Unfortunately, the underlying security of a blockchain is only as strong as its full nodes are decentralized:
Fewer full nodes =>
Fewer people validating transactions =>
Harder to detect a fraudulent transaction + Easier to collude and pass off fraudulent transactions as valid
Rollups and Layer 2s
Another scaling technique that has recently become popular are the use of rollups/layer 2s to scale the consensus layer of protocols such as Ethereum. Let's learn about layer 2s and see if they will be the answer to our scaling dilemma.
ZK Rollups
In the case of zk-Rollups, a Layer 2 (such as Scroll) executes transactions off-chain and generates a mathematical zero knowledge proof that proves the executed transactions have a certain (correct) execution result. The proof is then sent to an Ethereum smart contract which verifies the proof and updates the state of the layer 2 on chain. Critically, the amount of computation time required to verify the proof of the L2 transactions on Ethereum is much less than the computation time of just running the same L2 transactions on Ethereum directly. This means that zk-Rollups are able to scale the total number of blockchain transactions which have the security of Ethereum consensus, as the proof verifier runs directly on Ethereum and it is mathematically unfeasible to generate a "fake proof" (it is impossible to generate a proof with invalid/fraudulent transactions).
Unlike traditional blockchains, ZK Rollups don't just compute the global state transition resulting from a block of transactions, but also generate a succinct mathematical proof that proves the global state of the chain transitioned from the old state root (the blockchain's state before running the transactions in the block) to the new state root (the blockchain's state after running the transactions in the block).
This is interesting for our search for a horizontally scalable blockchain, as it allows us to avoid the "inverse correlation between TPS and security", since the work of blockchain nodes can be quickly verified without repeating the work of executing a block's transactions.
Optimistic Rollups

We applaud the Optimism team's honesty and agree with their evaluation:
Optimistic rollups have security that is not meaningfully different than an anonymous multisig.
In the spirit of #NotYourKeysNotYourCrypto, however, we will focus on zkRollups for the rest of our discussion.

Are zk-Rollups the solution to our scaling problems?
While zk-Rollups are set to shape the next decade of blockchain, an important caveat to keep in mind is that while rollups scale the number of users that can benefit from the security of Ethereum consensus, rollups do not scale the TPS of Ethereum. This is because transactions on Rollup A cannot directly call smart contracts on the Ethereum base layer or other Rollups deployed to Ethereum.
Let's consider a simple example to understand why Rollups do not scale Ethereum TPS in a conventional sense:
Note: for these scenario we will let:
Ethereum's block time in seconds, Number of Transactions in an Ethereum block
Rollup A's block time in seconds, Number of Transactions in a block on Rollup A
Rollup B's block time in seconds, = Number of Transactions in a block on Rollup B
Rollup C's block time in seconds, = Number of Transactions in a block on Rollup C
Note 2: It is worth noting that some projects have proposed cross-rollup/cross-chain bridges, and for the examples below the you could replace the Ethereum L1 with your cross chain bridge of choice.
Scenario 1: Normal Ethereum NFT Purchase
Bob has a balance of 1000 USDT on Ethereum
Sally has a balance of 500 USDT on Ethereum
Bob wants to buy an NFT for 1500 USDT from a marketplace on Ethereum
Sally sends Bob 500 USDT so he can afford the NFT
+1 Tx on Ethereum
Wait Duration
Bob uses the 1500 USDT to purchase the NFT from the NFT Marketplace smart contract
+1 Tx on Ethereum
Wait Duration
Summing up the transactions and wait durations, Scenario 1 required:
2 Transactions on Ethereum
Standard Wait Duration (If Bob submits his purchase transaction in the after Sally's transfer is confirmed)
Best Wait Duration (If Bob submits his purchase transaction in the same block that Sally sends the transfer in)
Scenario 2: "Cross-Rollup" NFT Purchase
Since existing Rollups have a finite block capacity and each block proof is posted to Ethereum, we need to add the rollup contributions to clogging up the Ethereum network amortized across all the transactions in a rollup block, so for each transaction on rollup we can say that 1 transaction requires Ethereum transactions.
Bob has a balance of 1000 USDT on Rollup A
Sally has a balance of 500 USDT on Rollup B
Bob wants to buy an NFT for 1500 USDT from a marketplace on Rollup C
Sally sends Bob 500 USDT on Rollup B
+1 Tx on Rollup B
+ Tx on Ethereum (Amortized cost of 1 Transaction on Rollup B)
Wait Duration
Bob withdraws the 500 USDT he received on Rollup B to his Ethereum wallet
+1 Tx on Rollup B (Request to bridge tokens back to Ethereum)
+1 Tx on Ethereum (Claim tokens on Ethereum)
+ Tx on Ethereum (Amortized cost of 1 Transaction on Rollup B)
Wait Duration
Bob withdraws his balance of 1000 USDT on Rollup A to his Ethereum wallet
+1 Tx on Rollup A (Request to bridge tokens back to Ethereum)
+1 Tx on Ethereum (Claim tokens on Ethereum)
+ Tx on Ethereum (Amortized cost of 1 Transaction on Rollup A)
Wait Duration
Bob deposits 1500 USDT from his Ethereum wallet into the Rollup C bridge contract
+1 Tx on Ethereum (Deposit into bridge contract)
Wait Duration
Bob buys the NFT on Rollup C for 1500 USDT
+1 Tx on Rollup C (NFT Purchase Transaction)
+ Tx on Ethereum (Amortized cost of 1 Transaction on Rollup C)
Wait Duration
Summing up the transactions and wait durations, Scenario 2 required:
1 Transaction on Rollup A
2 Transactions on Rollup B
1 Transaction on Rollup C
Transactions on Ethereum
Total Wait Duration
Best Wait Duration (if Bob processes his 1000 USDT withdrawal at the same time as Sally sends her 500 USDT transfer and Bob processes the 500 USDT withdrawal)
Scenario 3: Single rollup
Scenario 1: Normal Ethereum NFT Purchase
Sally has a balance of 500 USDT on Rollup A
Bob wants to buy an NFT for 1500 USDT from a marketplace on Rollup A
Sally sends Bob 500 USDT so he can afford the NFT
+1 Tx on Rollup A
+ Tx on Ethereum (Amortized cost of 1 Transaction on Rollup A)
Wait duration
Bob uses the 1500 USDT to purchase the NFT from the NFT Marketplace smart contract
+1 Tx on Rollup A
+ Tx on Ethereum (Amortized cost of 1 Transaction on Rollup A)
Wait Duration
Summing up the transactions and wait durations, Scenario 3 required:
2 Transactions on Rollup A
Transactions on Ethereum
Standard Wait Duration (If Bob submits his purchase transaction in block the after Sally's transfer is confirmed)
Best Wait Duration (If Bob submits his purchase transaction in the same block that Sally sends the transfer in)
Let's put the network usage in a table so we can see which scenario is most ideal, and why using rollups does not necessarily help scale Ethereum TPS:
| Scenario | # of Etherum Txs | # of Rollup A Transactions | # of Rollup B Transactions | # of Rollup C Transactions | Best Case Wait Time |
|---|---|---|---|---|---|
| #1: Ethereum/No Rollups | 2 | 0 | 0 | 0 | |
| #2: Multiple Rollups | 1 | 2 | 1 | ||
| #3: Single Rollup | 2 | 0 | 0 |
As we can see, not only did the multiple rollup scenario (Scenario 2) require strictly more L1 Ethereum transactions than just running the transactions on directly Ethereum (we made Ethereum less scalable 😭), and it also took much longer.
In scenario 3, where all the transactions were contained to a single rollup, we were able to execute our transactions with full Ethereum security, while requiring transactions on Ethereum. So long as is a big number, we are doing our part to help scale the security benefits of Ethereum consensus, while helping more people benefit from verifiable computing 🎉!
Now that we have a better understanding of the nuances of how rollups are related to scaling, Let's summarize what we have learned from our example scenarios:
We should contain our transactions to a single rollup and avoid cross-rollup transactions as much as possible
We want to maximize (number of transactions in a rollup block) to be very large, so that the Rollup's amortized transaction "cost" (in precious Eth mainnet EVM cycles) is as small as possible
We want (rollup blocktime) to be as short so our users don't have to wait a long time for their transactions to finish processing
The Awesomeness Score
It would be useful for us to have a single succinct metric that we can use to evaluate a rollup's ability to contribute to scaling Ethereum and improving Blockchain user experience. We can call this metric the Awesomeness Score -- a function of and . which:
returns a high score when:
is large (can process lots of transactions so we can put all our transactions on a single rollup)
.is small (users don't have to wait a long time for the block time finish)
returns a low score when:
is large (can't process many transactions at a time, so users will likely have to perform cross rollup transactions)
is small (users have to wait forever for their transactions to finish processing)
Fortunately, its easy to define such a metric which has these exact properties:
also reflects an important property that we did not fully consider in our above scenarios. Existing blockchains are serial, and can only process so many transactions in a given block time. Our scenarios assumed that the rollups themselves were not clogged up with transactions (if they were then we would have to wait until the queue of other transactions were finished processing before starting our wait time).
Great! It appears that rollups are the solution and all we need is a rollup with an that scales up with increased blockchain usage and we will finally have solved blockchain scaling!
Back to square 1?
Unfortunately, there are no existing zk Rollup blockchains with an that scales up with blockchain usage as we would like.
Additionally, if we look carefully at our key metric , it is actually just an expression for in disguise:

Hence, the only thing we have proved is that we will need to build a zk-Rollup with a scalable blockchain in order to use rollups to effectively scale the security of another blockchain's consensus.
Existing zk-Rollups, unfortunately, use the same architecture as Ethereum (zkSync, Polygon zkEVM, Scroll) or a similar serial state architecture (Starknet), so they will forever be asymptotically bound by their VM execution speed.
In other words, a rollup based on a zkVM with a serial state architecture can never be faster than an equivalent L1 running the same VM without ZK, because the zkVM equivalent needs to the execute the normal VM to generate the witness for the zk-proof. (Scroll/zkSync zkEVM will never have a higher TPS than the fastest normal EVM implementation)
The End of the Road?
So if Rollups and marketing juggernauts like Sui and Aptos aren't the answer, is it even possible to scale a general purpose blockchain?
It turns out, with the help of ZK, we can build a rollup which can scale horizontally and has a TPS that increases steadily with increased usage.
In our next blog post, we will design a new layer 2 from the ground up which resolves the key hurdles seen in previous blockchains:
Traditional smart contract state models risk race conditions unless we execute our VM in serial
- We will design a blockchain where writes by a given user are isolated to their own separate state tree, while allowing for global reads from the finalized state as it was at the last block.
The inverse correlation between TPS and Security
- We will design our scalable blockchain from the ground up around ZK, so that the result of each parallel computation is a succinct proof that can be verified in much faster than rerunning the transactions.
"Many Rollups" dilemma
- We will design our blockchain to be hyper scalable and have a single, easily verifiable global state, removing the need for cross rollup transactions entirely
Below we can see a sneak preview of how such a blockchain can be designed: