- Published on
ZK + PARTH: An Architecture for Building Horizontally Scalable Blockchains
- Authors

- Name
- Carter Jack Feldman
- @cmpeq
ZK + PARTH: An Architecture for Building Horizontally Scalable Blockchains
In this post, we re-invent QED's horizontally scalable blockchain architecture from first principles.
Please read our blog post "The Blockchain Scaling Dilemma" before starting this article, it is highly recommended prerequisite reading, and we will refer to it throughout the following post.
Background
As we discussed in our previous post, the key barriers which have thus far hindered attempts at scaling blockchains securely are:
The inverse correlation between TPS and Security
- On traditional blockchains, any increase in parallelization/scalability leads to a proportional decrease in decentralization/security as increasing scale also increases the barrier of entry for running full nodes.
Traditional smart contract state models risk race conditions unless we execute our VM in serial
- Recall the token contract example from the previous post
"Many Rollups" dilemma
- If we try to scale a blockchain with many low TPS rollups, users are necessarily fragmented across different rollups, and we end up with more rather than less on chain transactions because we can't directly call smart contracts on rollup A from rollup B
In the past, many blockchains have tried and failed to overcome these barriers in the pursuit of massively parallel transaction processing, let's see if we can crack the code.
To tackle this challenge, we will first find solutions to each of these problems individually, and the design a blockchain from the ground up which combines them to give us an architecture for a horizontally scalable blockchain.
Solving "The inverse correlation between TPS and Security"
As we discussed in our previous post, Full Nodes on most existing blockchains (for example, Ethereum) have to process every transaction executed on the network. This is to ensure that each full node can be certain of what the current blockchain's state is without trusting any third parties.
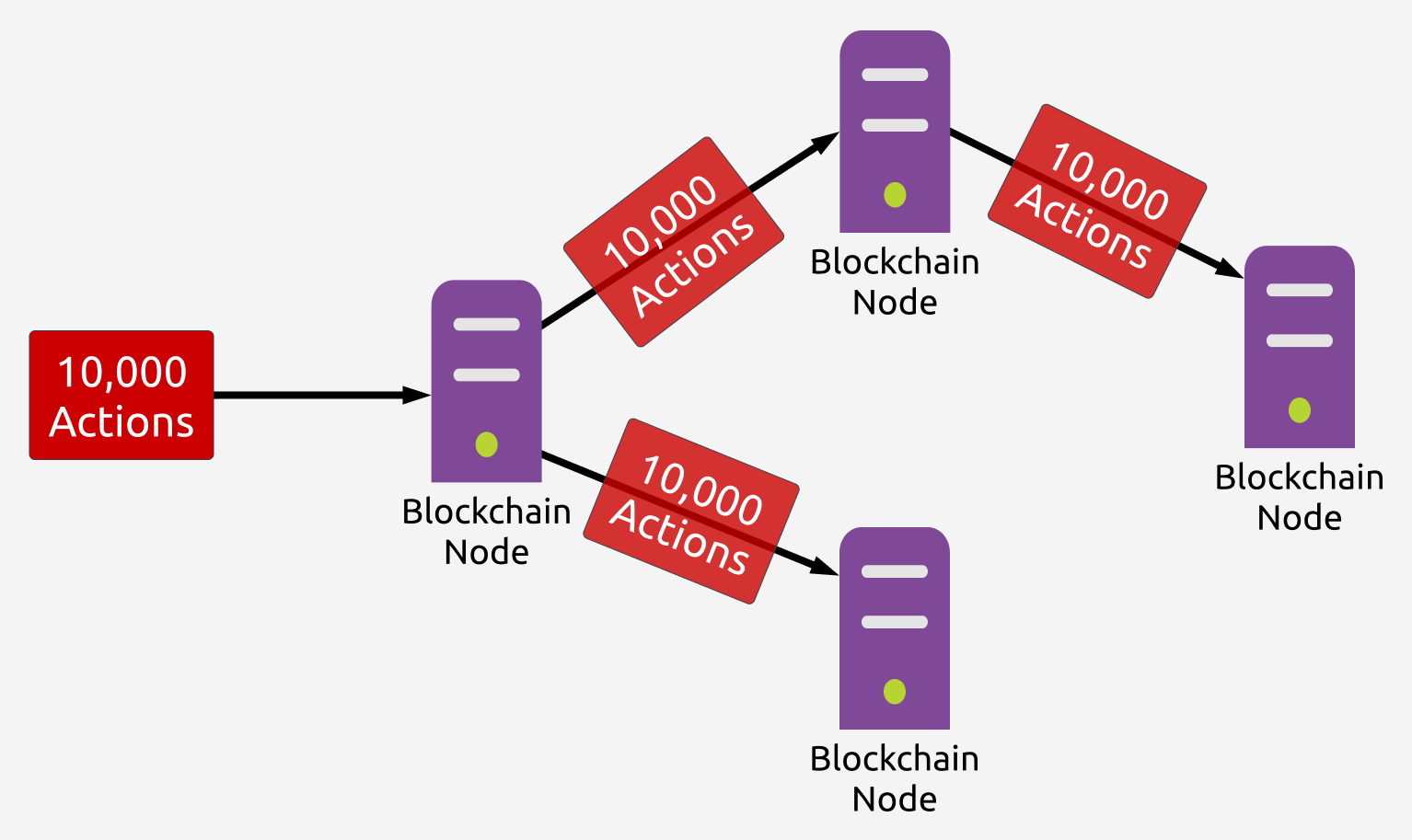
This has a practical implication that the network can only process transactions as fast as its slowest full node, as otherwise the slowest full node would fall out of sync with the rest of the network -- this is not going to work if we want to build a scalable blockchain (higher the TPS = higher the barrier of entry to start a full node = less nodes participating in the network = less secure).
In our previous post, we also discussed the existence of chains which take a different approach, instead spliting up the transactions in a block into batches, and processing each batch of transactions in parallel. As we saw in our previous post, this leads to some increase in TPS over chains like Ethereum, but in practice does not move the needle much due to race conditions that force serial execution.
In addition, this doesn't solve the security issue of further centralization, as it means only a portion of the total nodes on the network process each transaction:
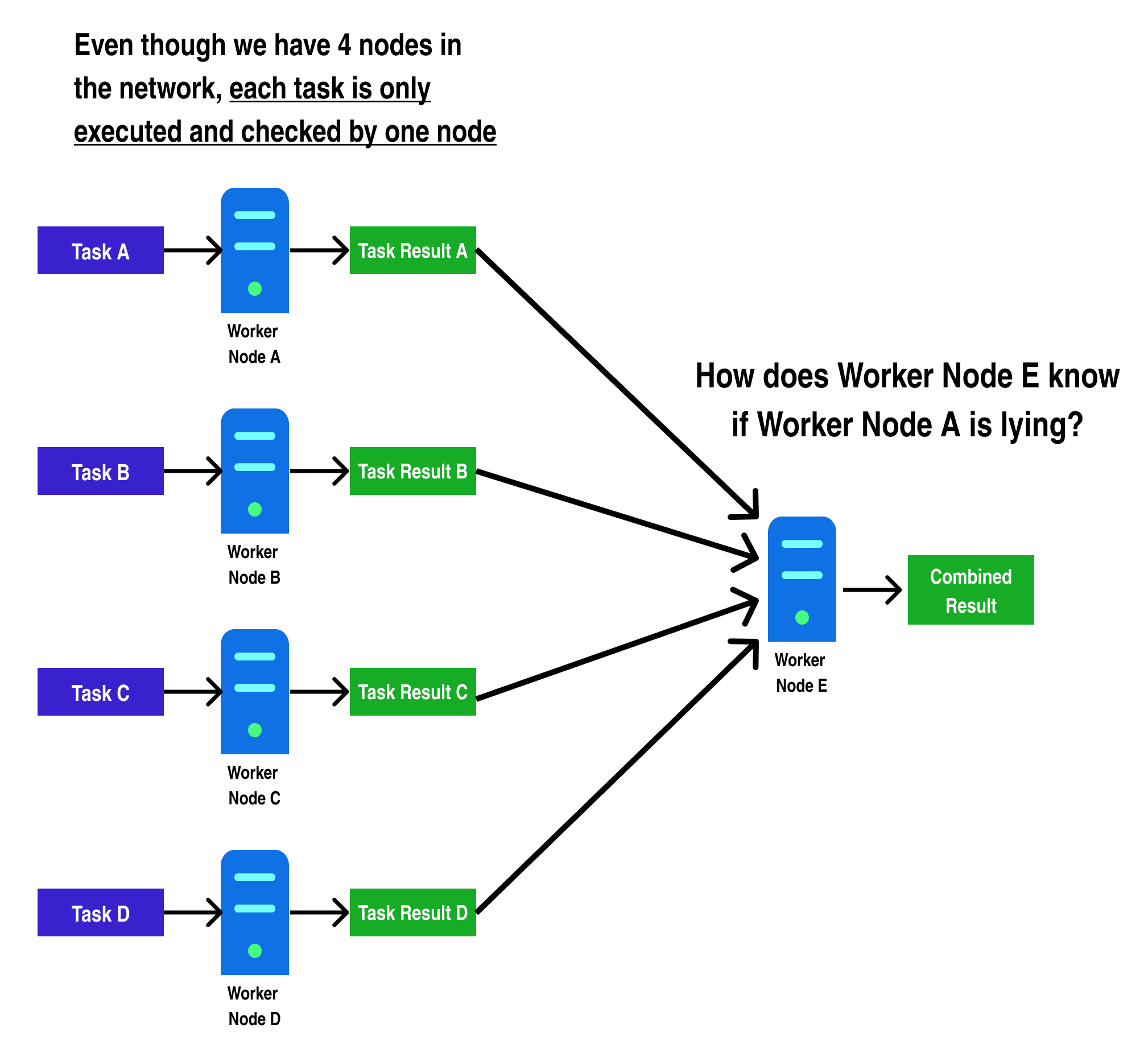
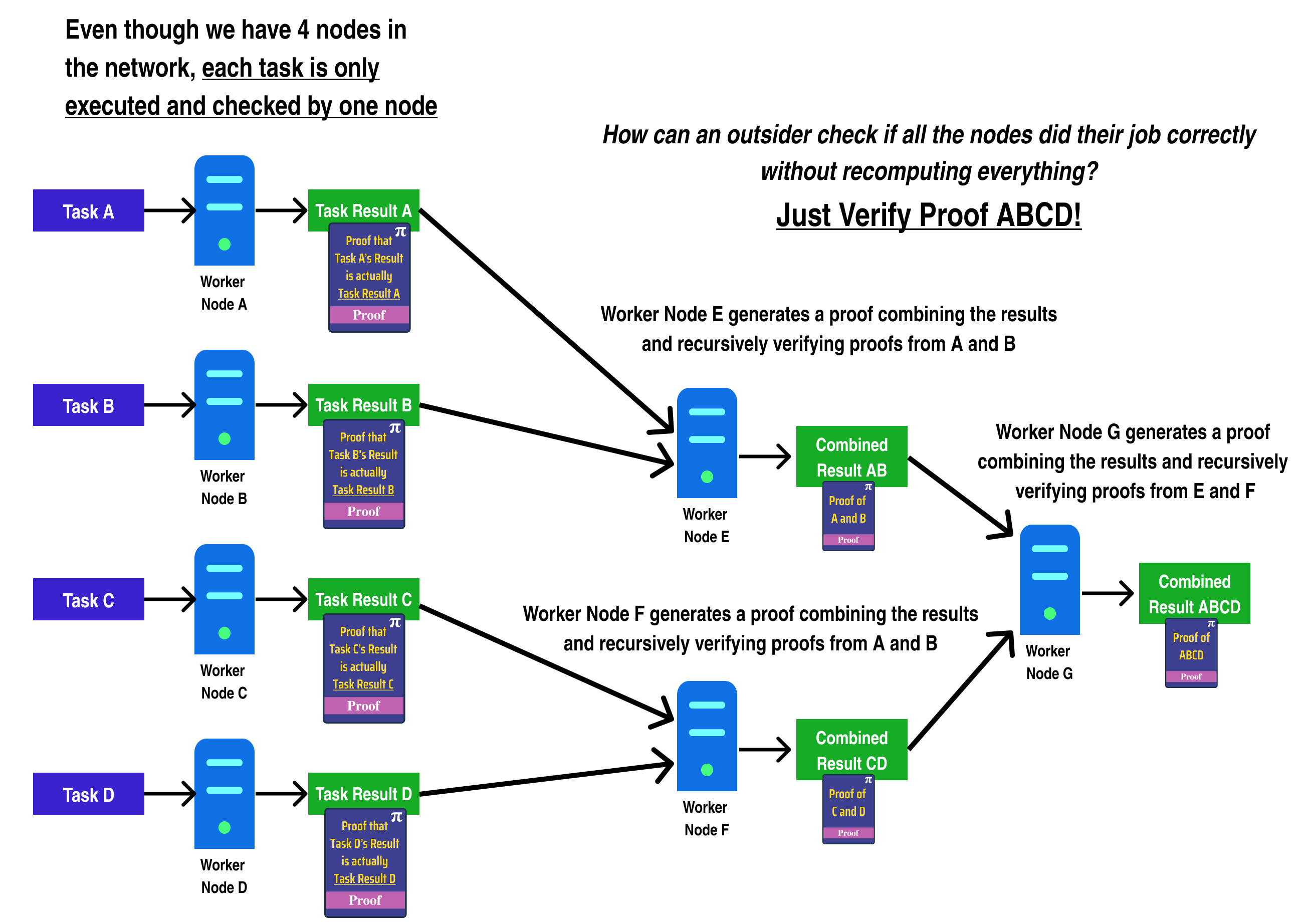
In the diagram above, we can see a generalized example of the problem faced by blockchains which try to implement parallelism. For standard blockchains, the only way for Worker Node E to check if Worker Node A computed Task A correctly would be to recompute Task A again and compare the results!
Hence, to achieve the same security guarantees on a chain making use of parallelism with n nodes as an Ethereum chain with the same number of nodes, each node would have to re-do every other node's work, making the "parallelism" disappear, as each node ends up having to compute each transaction to be sure of the block's end state.
One way to resolve this issue is by having Worker Node A/B/C/D generate a Zero Knowledge Proof which proves they computed their respective tasks correctly. Among other things, Zero Knowledge Proofs allow for a worker to generate a proof that some arbitrary computation was executed correctly and returned a result. Crucially, there exist Zero Knowledge Proof systems where the proof can be verified in far less time than it takes to run the original computation, meaning that each worker node can check each others work very quickly:
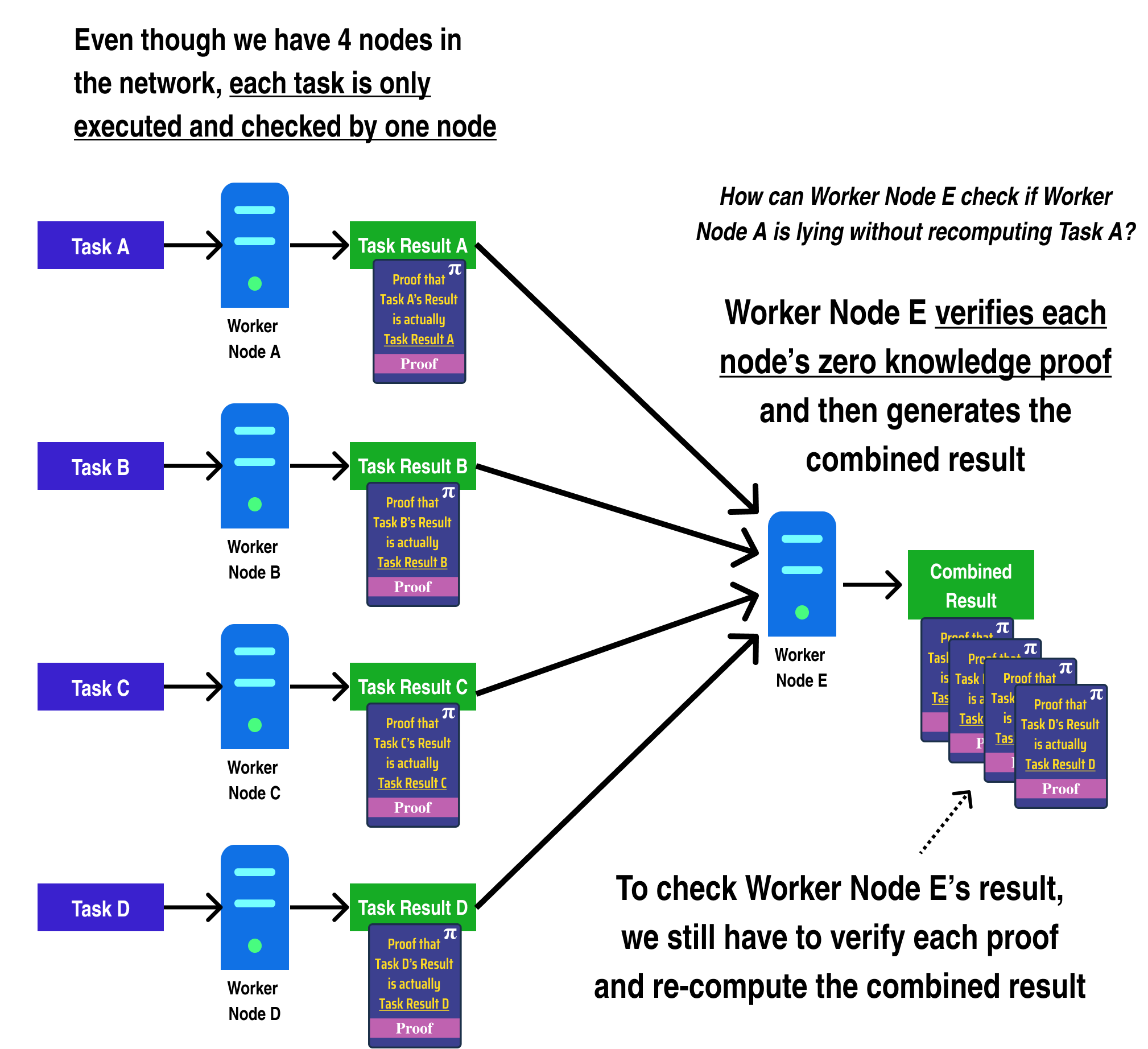
In fact, we can go one step further and generate a zero knowledge proof which proves a computation in addition to verifying several other zero knowledge proofs:
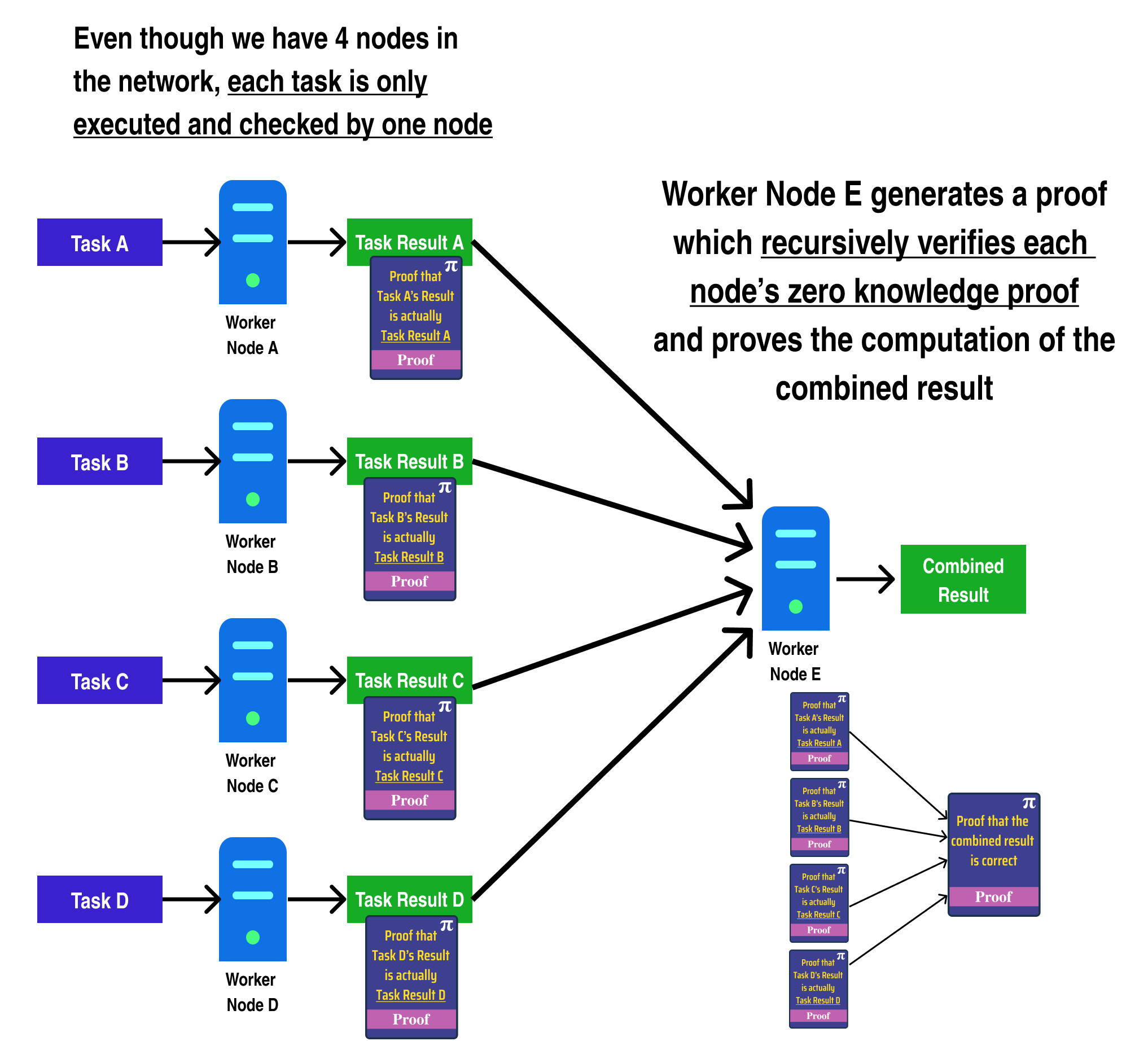
Anyone can verify the correctness of the combined result by verifying the combined result proof generated by Worker Node E.
In the diagram above, however, the proving time of Worker Node E grows linearly with the number of worker proofs it needs to verify. We can fix this by making use of tree recursion, and splitting the combine operation into two distinct computations:
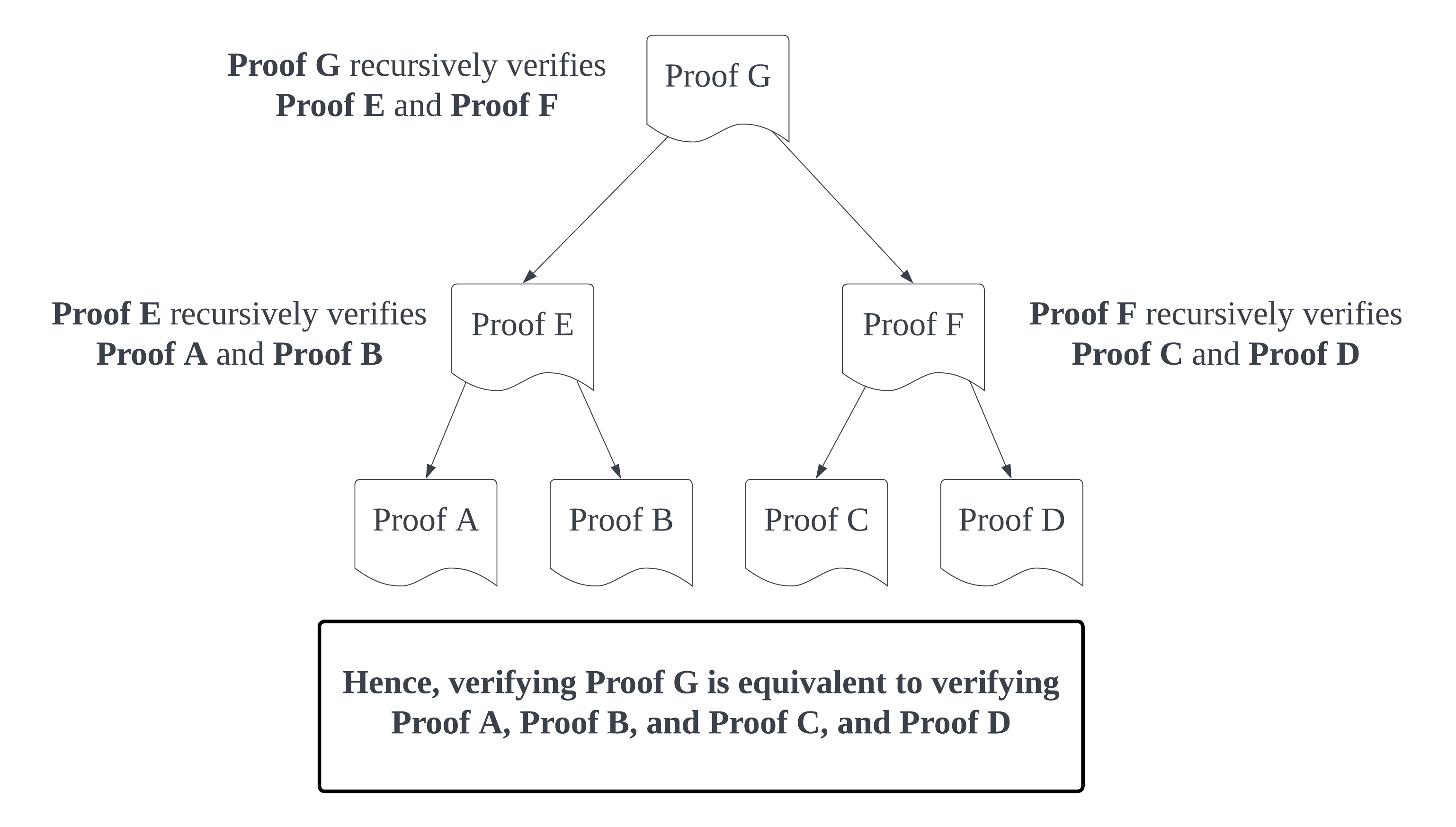
Applying tree recursion to our original diagram, we can see a finished example of how a scalable, verifiable process could be architected where the time it takes to generate a finished proof is for tasks:
Now that we have a rough idea of how to architect a scalable, trustless system, let's start designing our horizontally scalable blockchain.
A framework for inventing our new blockchain
When addressing a difficult problem like building a blockchain that horizontally scales, it is often useful to see if we can reduce the scope of the problem by asking ourselves why we want to solve the problem in the first place.
Why does the world need a horizontally scalable blockchain?
In the case of building "a blockchain that horizontally scales to 1,000,000+ TPS", we want to enable millions of users around the world to interact with the blockchain, much like they do with applications and services on the internet (ie. realize the vision of web3).
Since individual internet users do not make millions of requests per second in web2, we can narrow the scope of our blockchain to "a blockchain capable of a supporting millions of concurrent users, each transacting at a few transactions per second".
With our new problem scope, we still will need to build a blockchain which can support millions of transactions per second, but we now know that we do not have to consider the case where a single user needs to send millions of transactions per second:
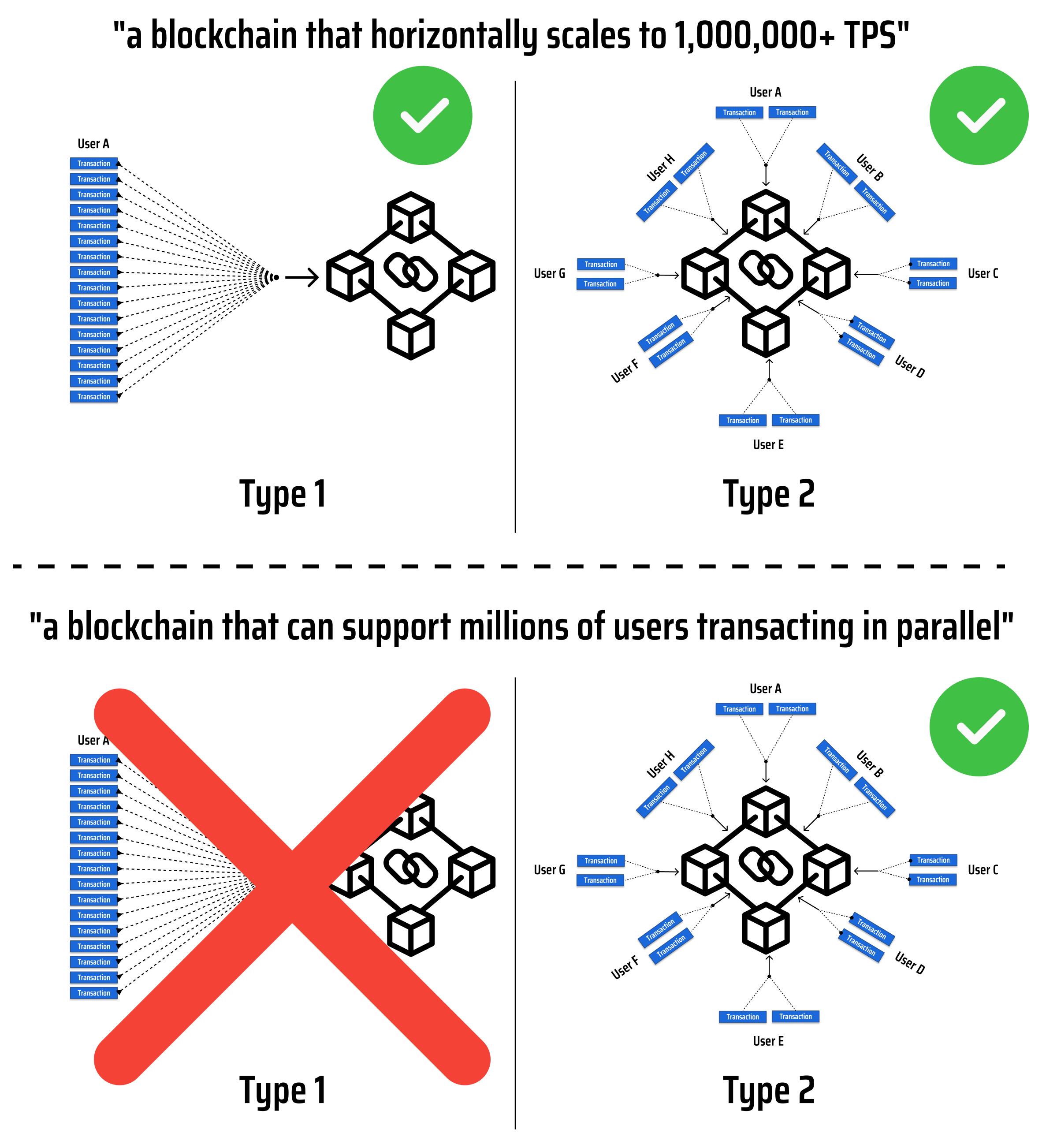
In the diagram above, both type 1 and type 2 cases process the same number of transactions, with the caveat that, in type 1, all the transactions come from the same user. Based on our refined goal, we only need to support type 2!
The Skeleton of a Horizontally Scalable Blockchain
Now that we have narrowed our to "a blockchain that can support millions of users transacting in parallel", let's iterate our diagram and try to discover an architecture that makes sense:
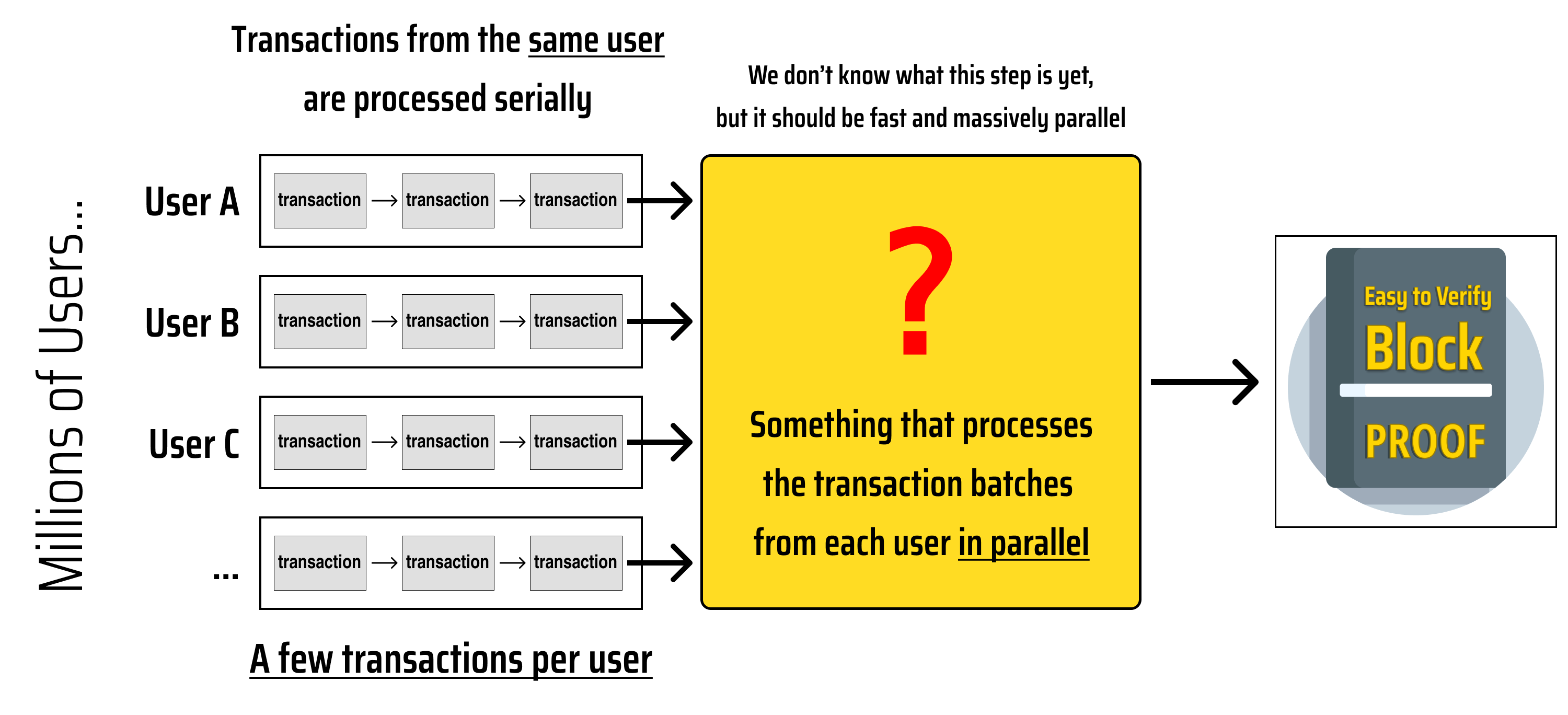
To help us avoid the "inverse correlation between TPS and security" that has plagued other blockchains, we can use what we have learned about tree recursion in the previous section to fill in the gaps in our diagram:
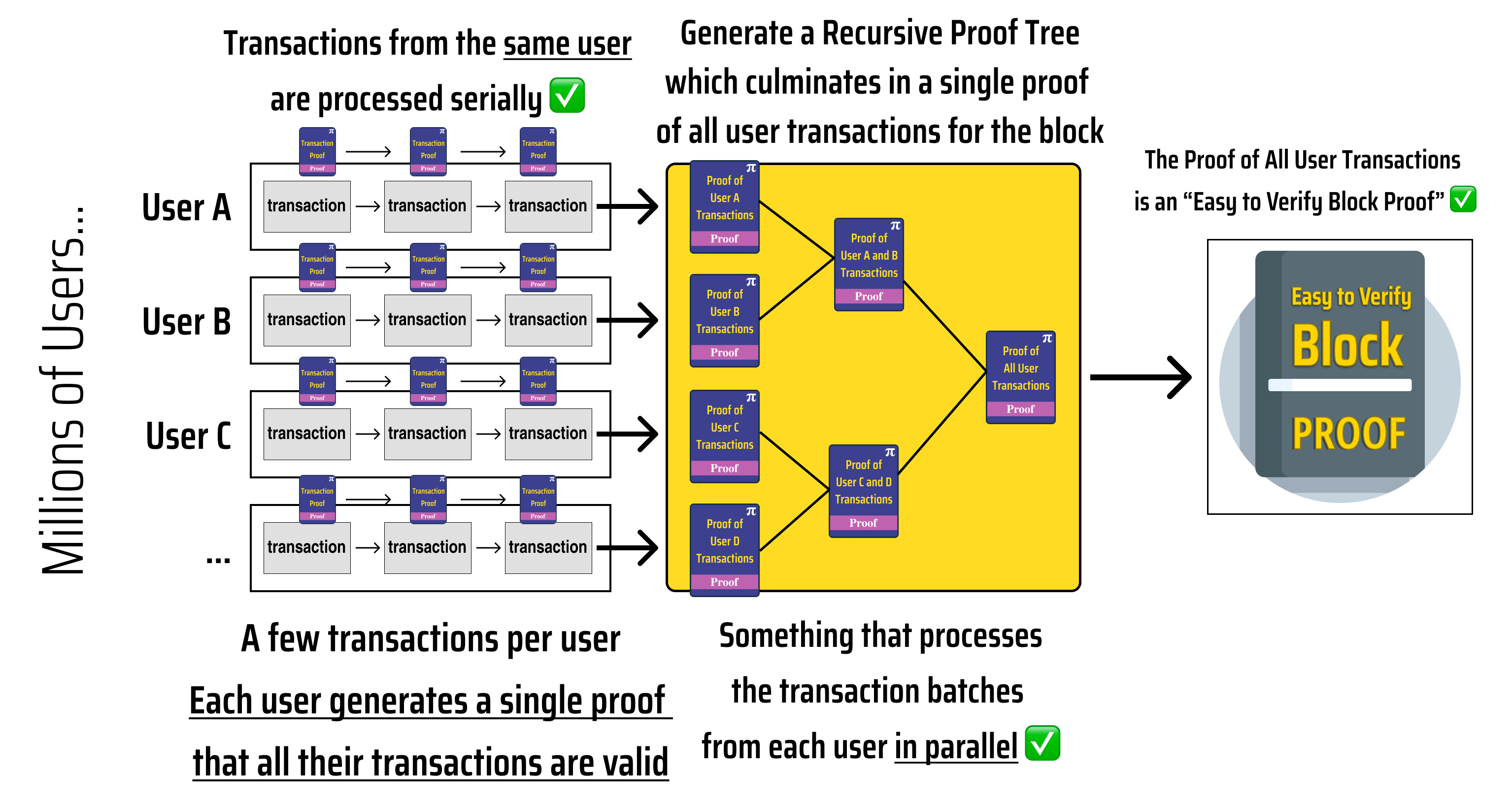
Looking at the diagram above, we can see that:
Each user transaction proves the transaction result and recursively verifies the previous user transaction.
- Proving User X's transactions takes time where is the number of transactions made by User X in the block
The user transactions are aggregated into a single proof of all transactions in the block using tree recursion
- Generating the block proof takes time where is the number of users participating in the block
Quantifying our new blockchain's block time
Let's use our diagram to come up with a formula for our block time so we can better analyze how it scales up.
To help quantify our block time, we need to first define some variables:
the time it takes (in seconds) to execute and prove one transaction
The time it takes (in seconds) to generate a proof which recursively verifies and combines the result of two other proofs
The time it takes (in seconds) to send a proof from one node to another
The maximum number of transactions executed by a single user during the block
The total number of users participating in a block
If we annotate our diagram with these variables, we can get a better idea of how to quantify our block time:
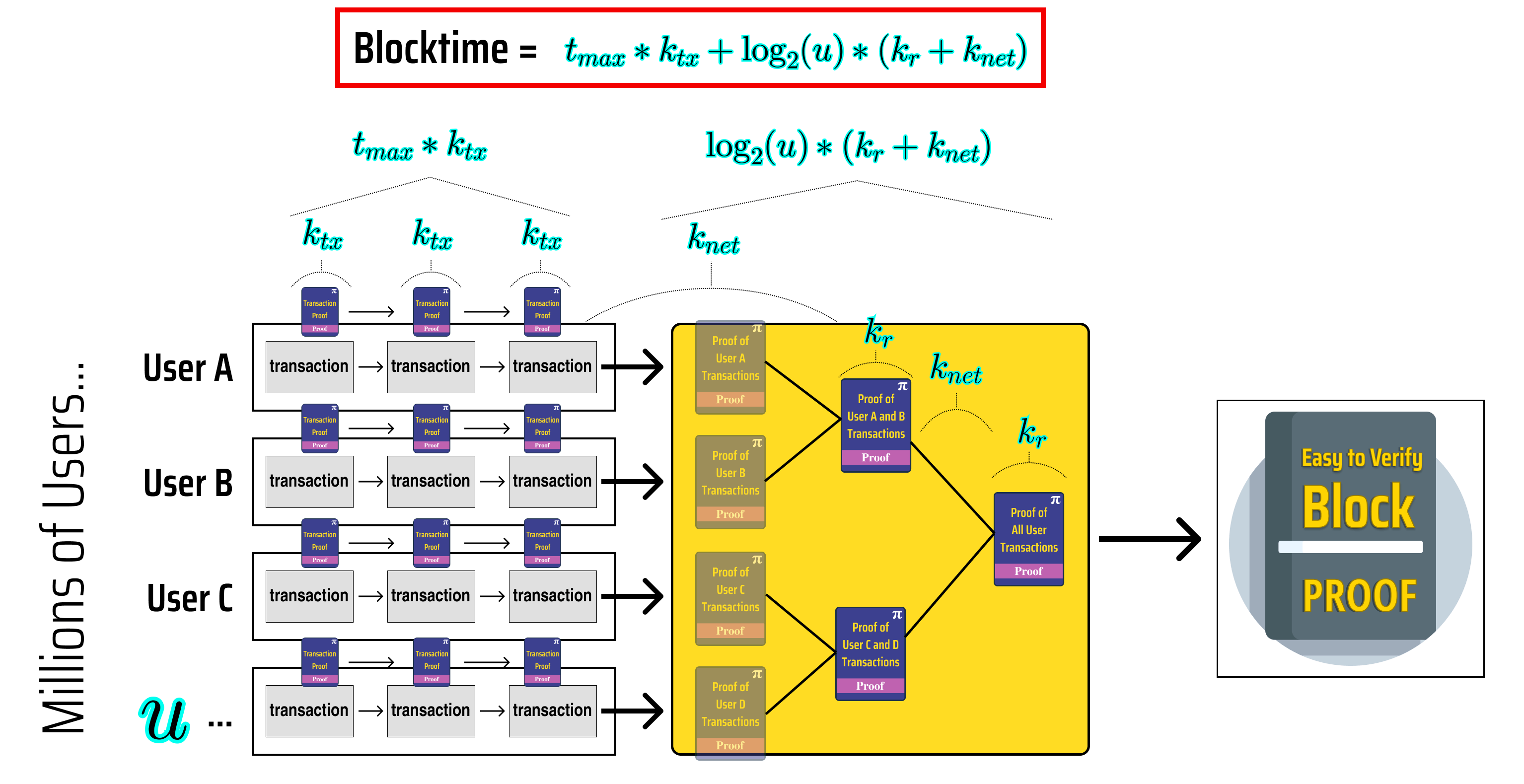
On the left side of our diagram, we can see that each user takes at most seconds to generate their final transaction proof, and that the time it takes to generate our block proof once we have proved each user in parallel is , hence our block time can be given by:
Assuming that each user proves the same number of transactions, we can also write a formula for TPS, since we know that each user executes transactions and that there are users participating in the block:
Since QED has already built a blockchain which implements a similar architecture, we can also plug in known conservative values for our variables so we can see how our proposed architecture scales with respect to users:
Time to Prove a Transaction: <300ms
Time to send a proof (30kb) to another node: <100ms
Time to generate a proof which recursively verifies and combines the result of two other proofs: <250ms
In addition, we want to support a blockchain where lots of users can make a few transactions each per block, so we can conservatively say (each user submits 3 transactions per block).
Plugging in our experimental values, we get a formula for our block time and TPS which are functions of the number of users submitting transactions in a block:
Traditional serial blockchains' TPS is limited by the single threaded CPU clock speed, and since this number is constant for our nodes, TPS also has a constant upper limit for traditional serial blockchains.
The evm-bench project provides replicable benchmarks that give us an indication of the theoretical upper limit on Ethereum TPS given current hardware:
| Function | evmone | revm | pyrevm | geth | py-evm.pypy | py-evm.cpython | ethereumjs |
|---|---|---|---|---|---|---|---|
| erc20.mint | 5ms | 6.4ms | 14.8ms | 17.2ms | 334ms | 1.1554s | 3.1352s |
| erc20.transfer | 8.6ms | 11.6ms | 22.8ms | 24.6ms | 449.2ms | 1.6172s | 3.6564s |
Using the erc20.mint as a benchmark, EVM's theoretical upper limit on current hardware is around 200 TPS ().
With the assumption that each users makes 3 transactions, we can write a formula for EVM chain block time as a function of number of users as well:
Let's graph our architecture's block time and the theoretical minimum block time for EVM chains and see how they scale with increased usage:
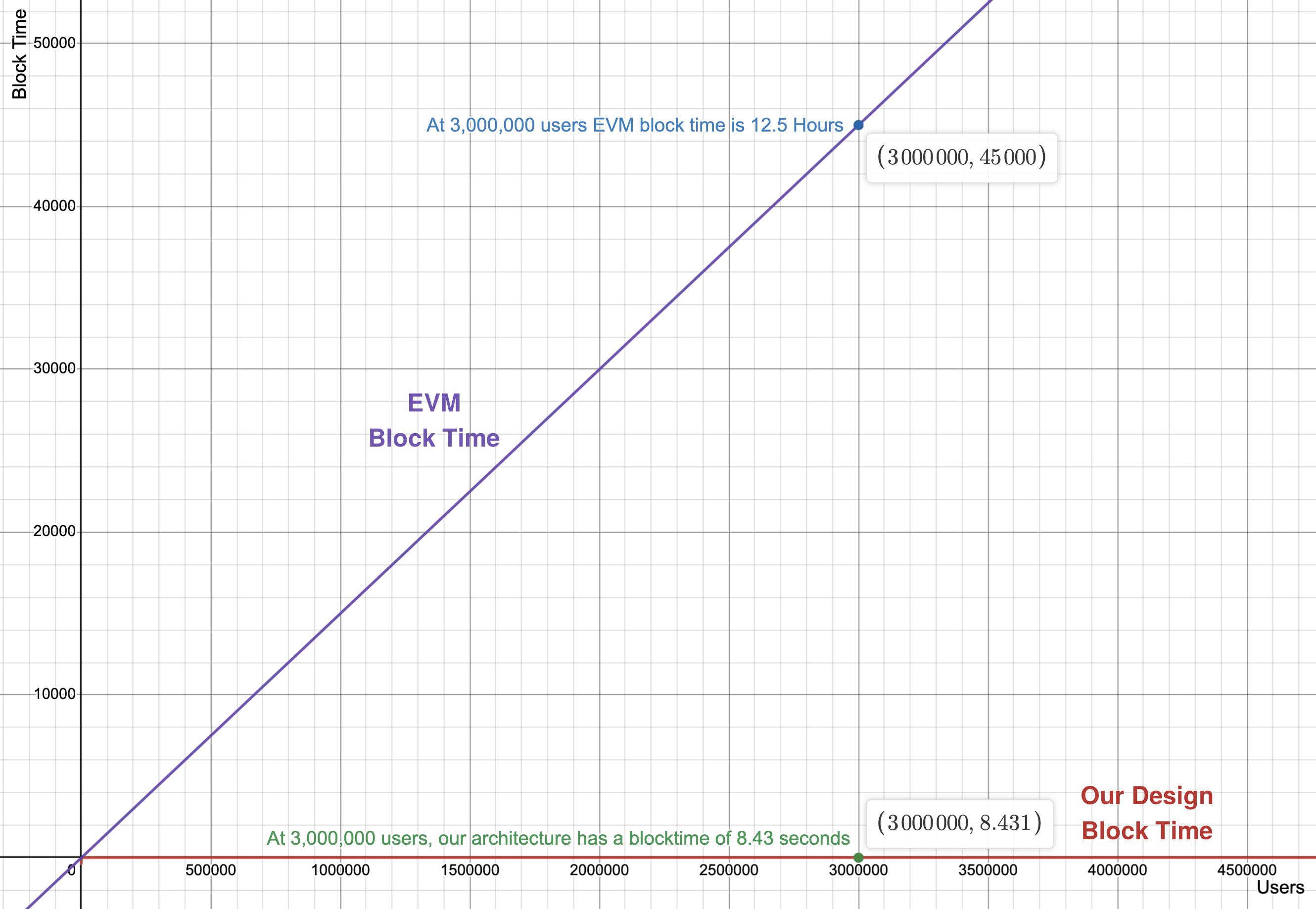
With a load of 3,000,000 users (a reasonably sized multiplayer game), EVM chains would take 45,000 seconds to produce a block (12.5 hours), while our new design would only take 8.431 seconds! This means, if we want 3,000,000 users on an EVM chain to submit a few transactions, the users would need to wait over 12 hours for their transaction to process!
Let's also calculate what our designed architecture's TPS would be at the 3 million user mark:
Great 🎉, we have invented a blockchain architecture which can handle 1,000,000+ TPS without succumbing to the "Inverse Correlation between TPS and Security".
Let's update our problem list to see what is left before we can call ourselves a secure and horizontally scalable blockchain:
The inverse correlation between TPS and SecuritySolved ✅- Solved using our recursive proof architecture ✅
Traditional smart contract state models risk race conditions unless we execute our VM in serial ❌
- We still need to solve this
"Many Rollups" dilemmaSolved ✅- We have avoided the many rollups dilemma by architecting a single rollup capable of handling 1,000,000+ TPS
We are not done, however, as we still have yet to tackle race conditions.
Solving Race Conditions with PARTH
Since we are designing a blockchain architecture from scratch, we have the freedom to completely revamp how our blockchain's state is modeled. With that said, we need to design a state model which fits our earlier parallelization example.
A helpful way to design a race condition free system for a process diagram like the one we designed earlier is to mark each process node with the data it needs to write:
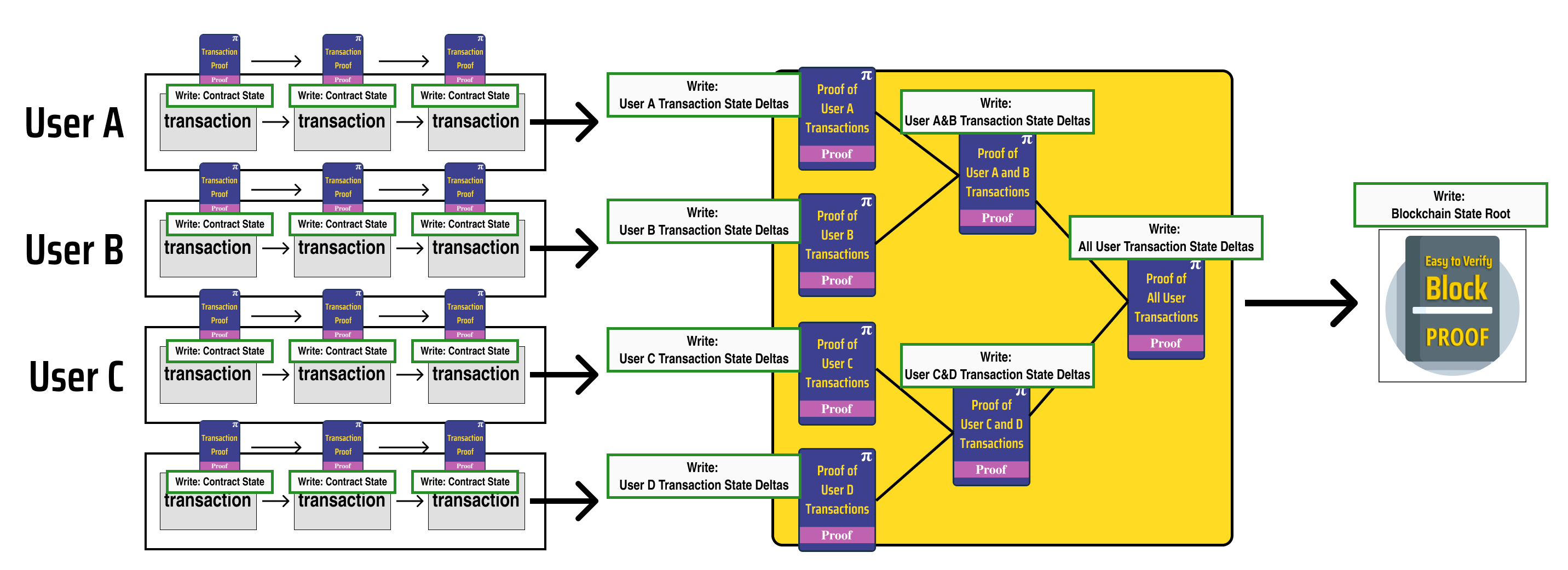
Since we want to ensure that our parallel tasks can execute without race conditions, we need to ensure that no two parallel processes can write to the same state value (consider the race condition example in our previous post).
Let's indicate this by drawing dashed red lines which enforce write separation between parallel processes:
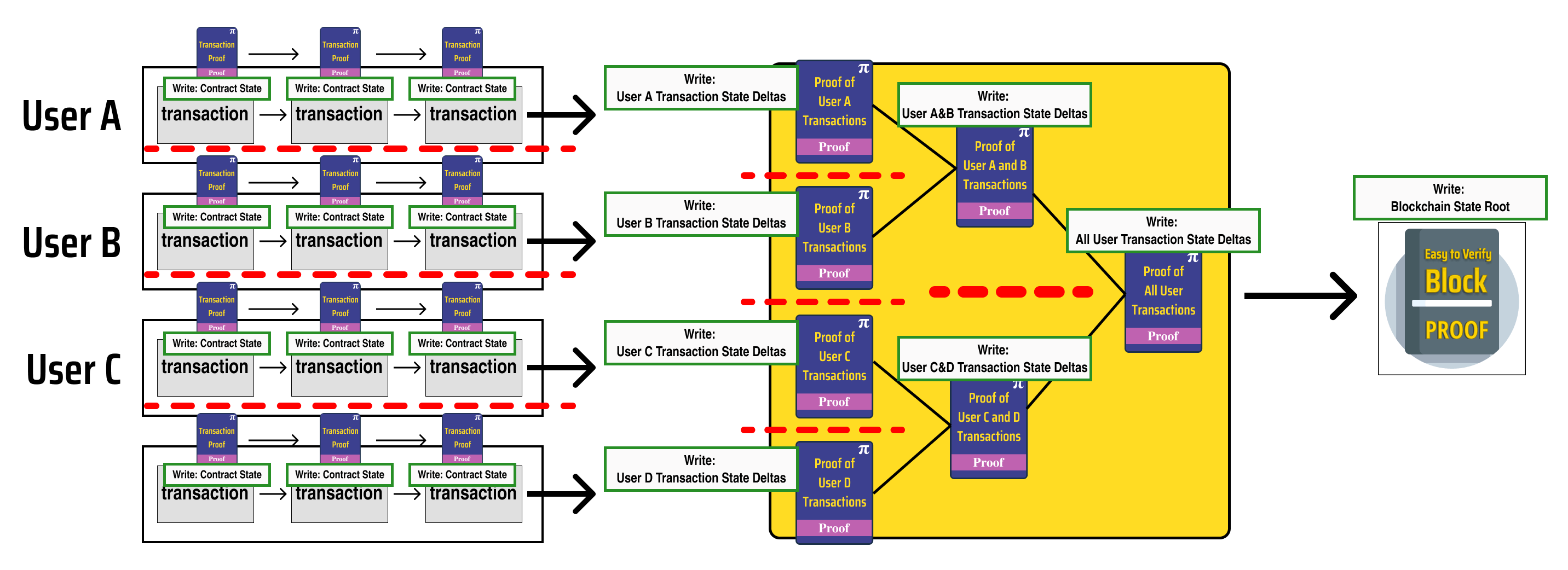
Notice that the processes in the diagram fall into 3 distinct groups based on the type of state data they update and the logic which governs their execution:
Processes which update contract states
- Updates are determined by smart contract logic
Processes which update user states
- Updates are determined by the recursively verified proofs which update contract states
Processes which update the state root of the blockchain
- Updates are determined by the recursively verified proof which updates all the user states
We will call these distinct process groups PARTH groups, and we can label them in the diagram:
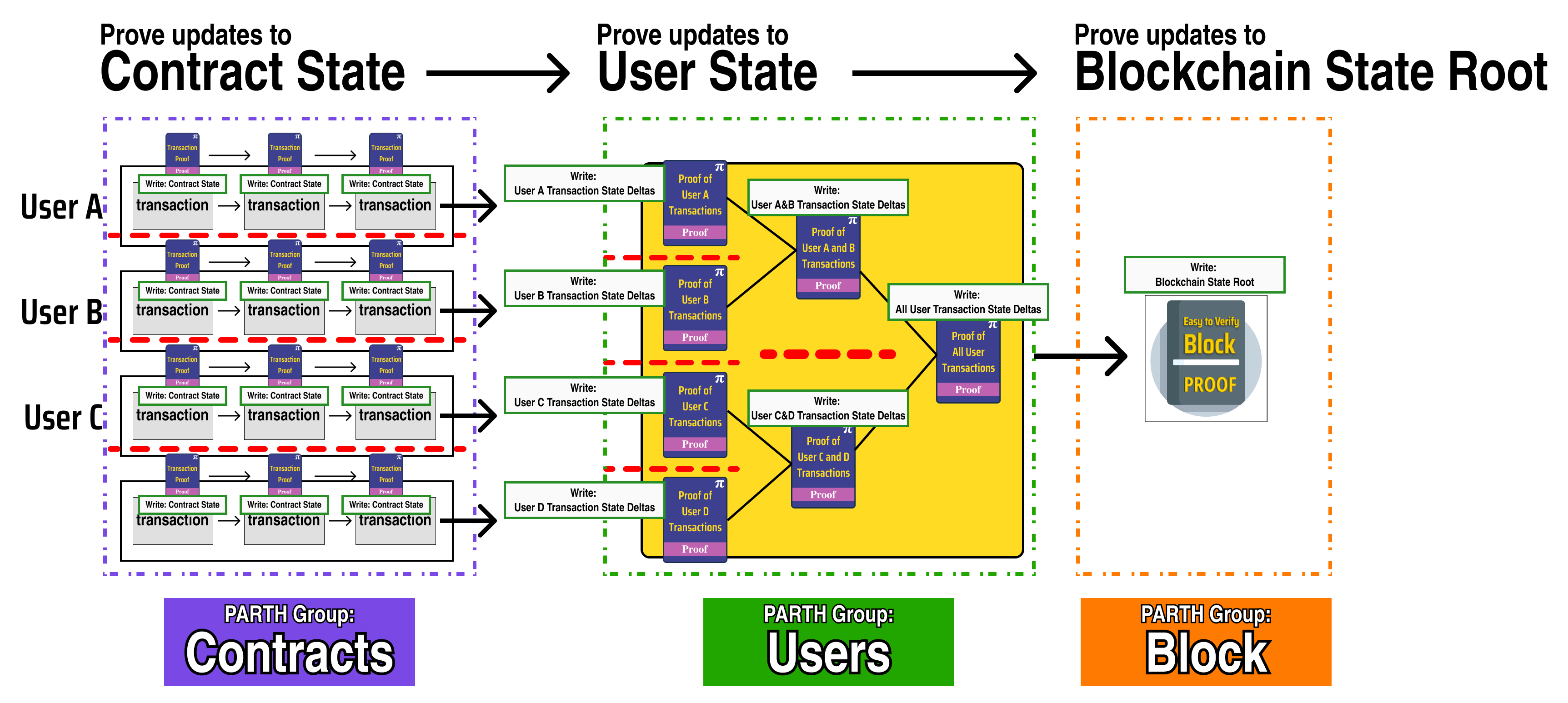
In our new diagram, we can see that each PARTH group starts by recursively verifying the end proof of the previous PARTH group:
The first step in the Users PARTH group recursively verifies the proof generated by the last parallel step in the Contracts PARTH group
The first step in the Block PARTH group recursively verifies the proof generated by the last parallel step in the Users PARTH group
This end-to-end recursion guarantees that anything proved in an earlier PARTH group is also verified and proved by the final PARTH block proof, meaning that the integrity of all the parallel computations is preserved with the security of the underlying proof system. Keep this in mind as we begin to explore PARTH and its implications as we design our race-condition free state topology.
PARTH
PARTH is an acronym that stands Parallel Ascending Recursive Tree Hierarchy, and it is a general framework for architecting race condition free parallel processes and their accompanying state topology.
The main idea of PARTH is that we design our state topology to mirror the structure of our recursive proofs.
We can see why we call it PARTH by rotating the diagram we made previously and seeing the revealed proof tree hierarchy:
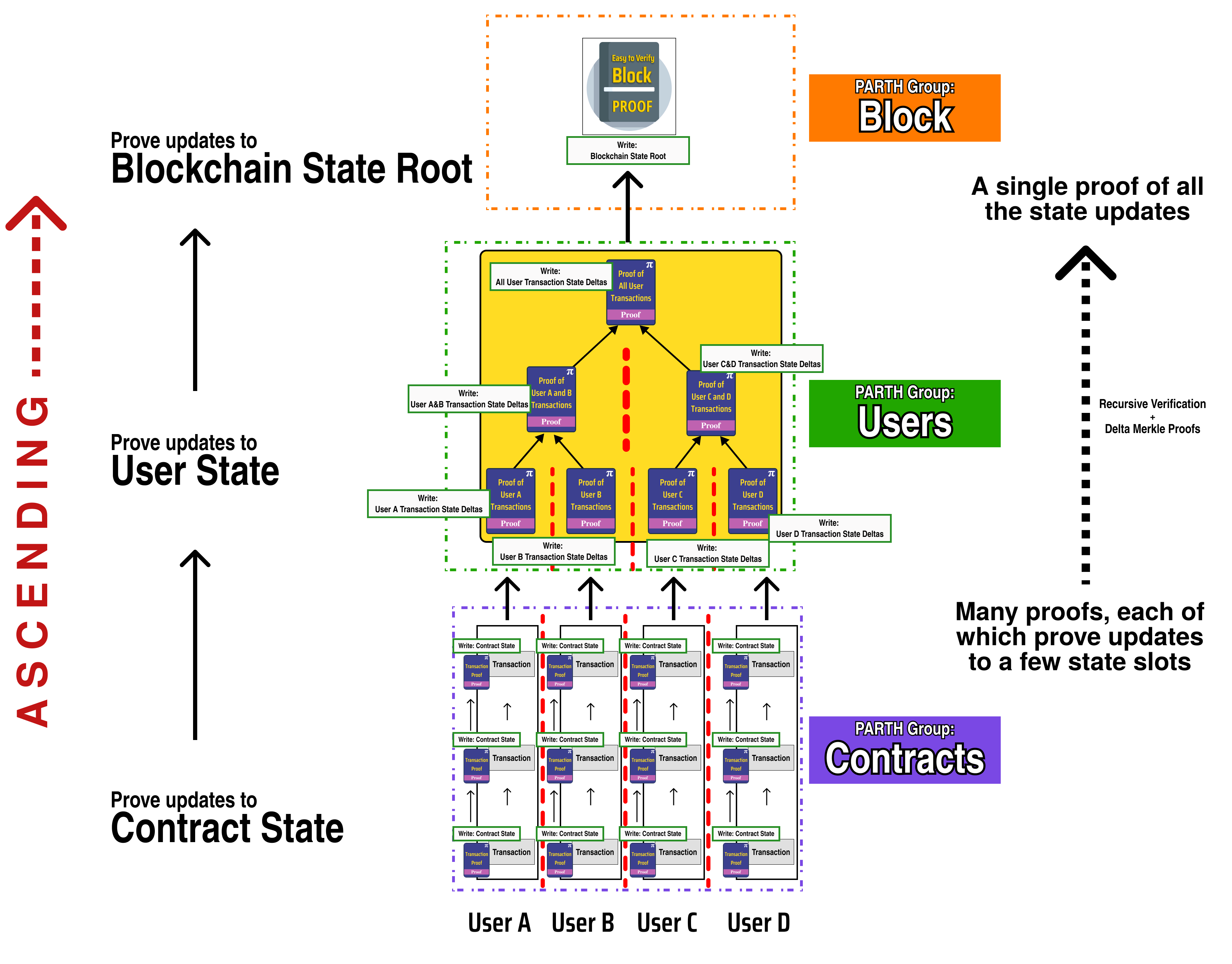
In addition to prescribing a process flow for our parallel block construction, PARTH also tells us how we should organize our state so as to ensure no write race conditions can occur (since the proving topology mirrors our state topology, parallel nodes are . Specifically, PARTH prescribes that the state topology have the same hierarchy as our PARTH groups:
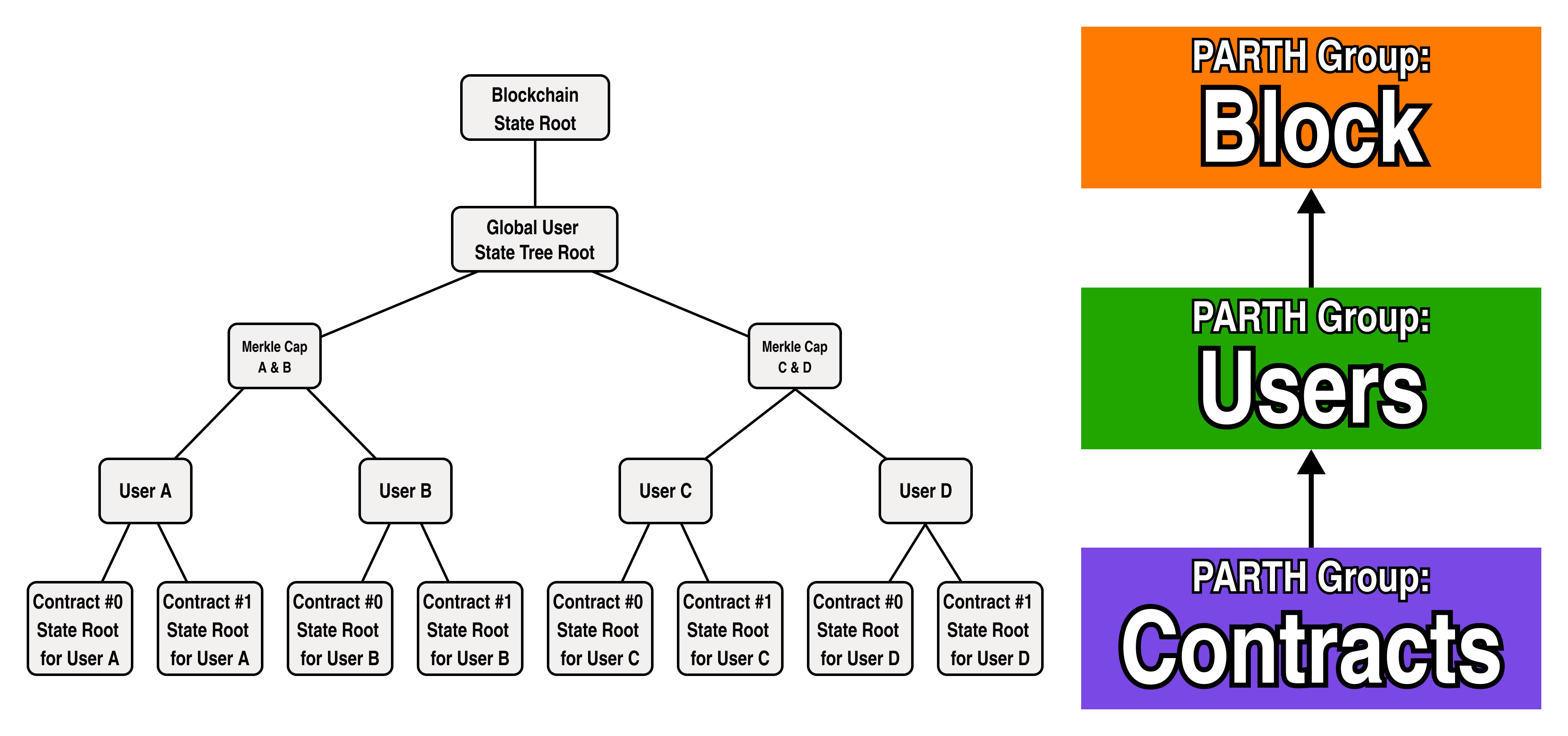
In our architecture, each PARTH group has a common set of logic and constraints which govern updates to a portion of the global state tree. With that in mind, let's try to color our nodes based on our previous diagrams:
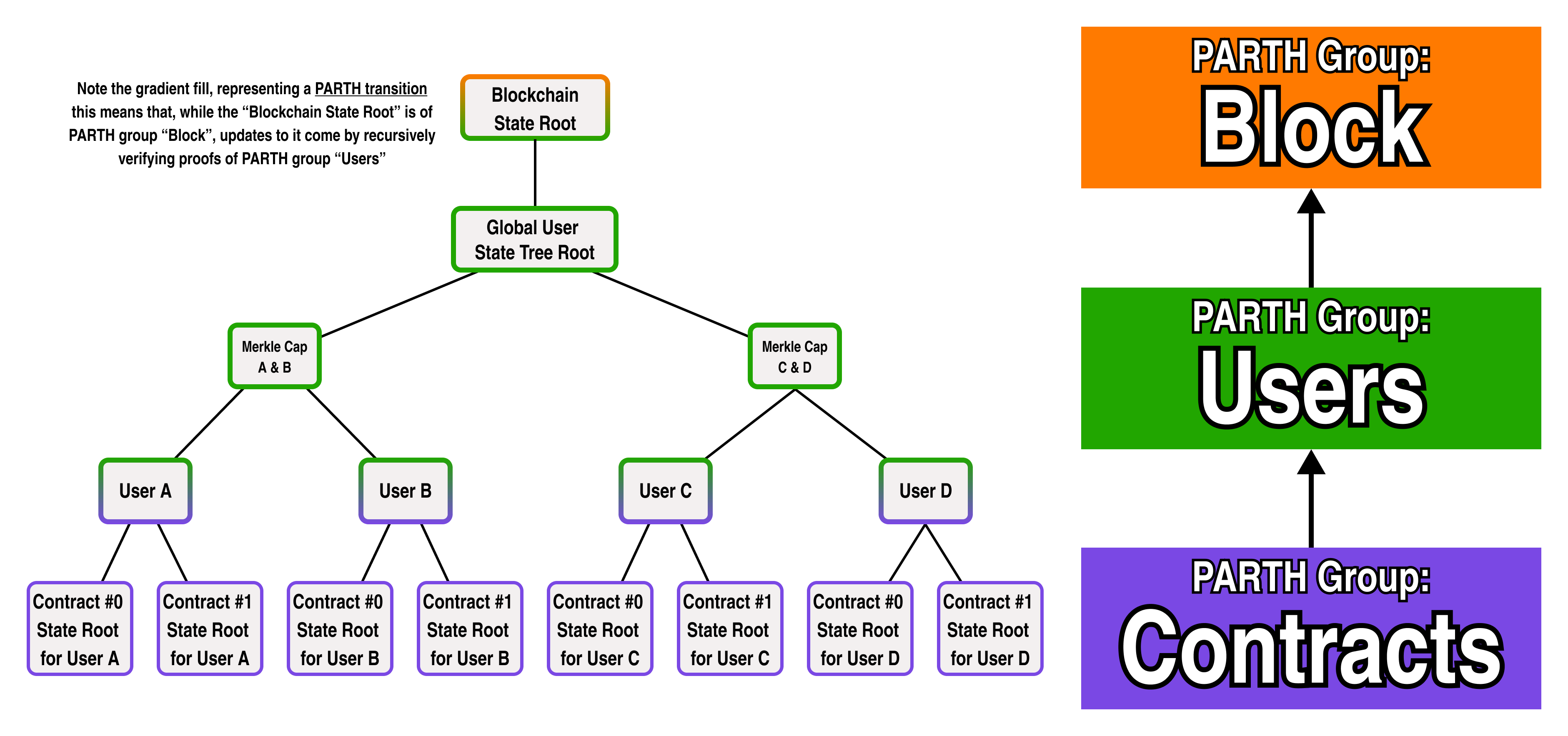
Recalling that all the nodes in a PARTH group share a common set of update logic, however, something is clearly amiss.
If we look at the diagram closely, the state roots of a contract do not actually share a common "Contracts" logic-- as each smart contract has its own separate logic. Since each user has a separate tree, let's rename the "Contracts" PARTH group to "User State", and add two separate PARTH groups for Contract 0 and Contract 1:
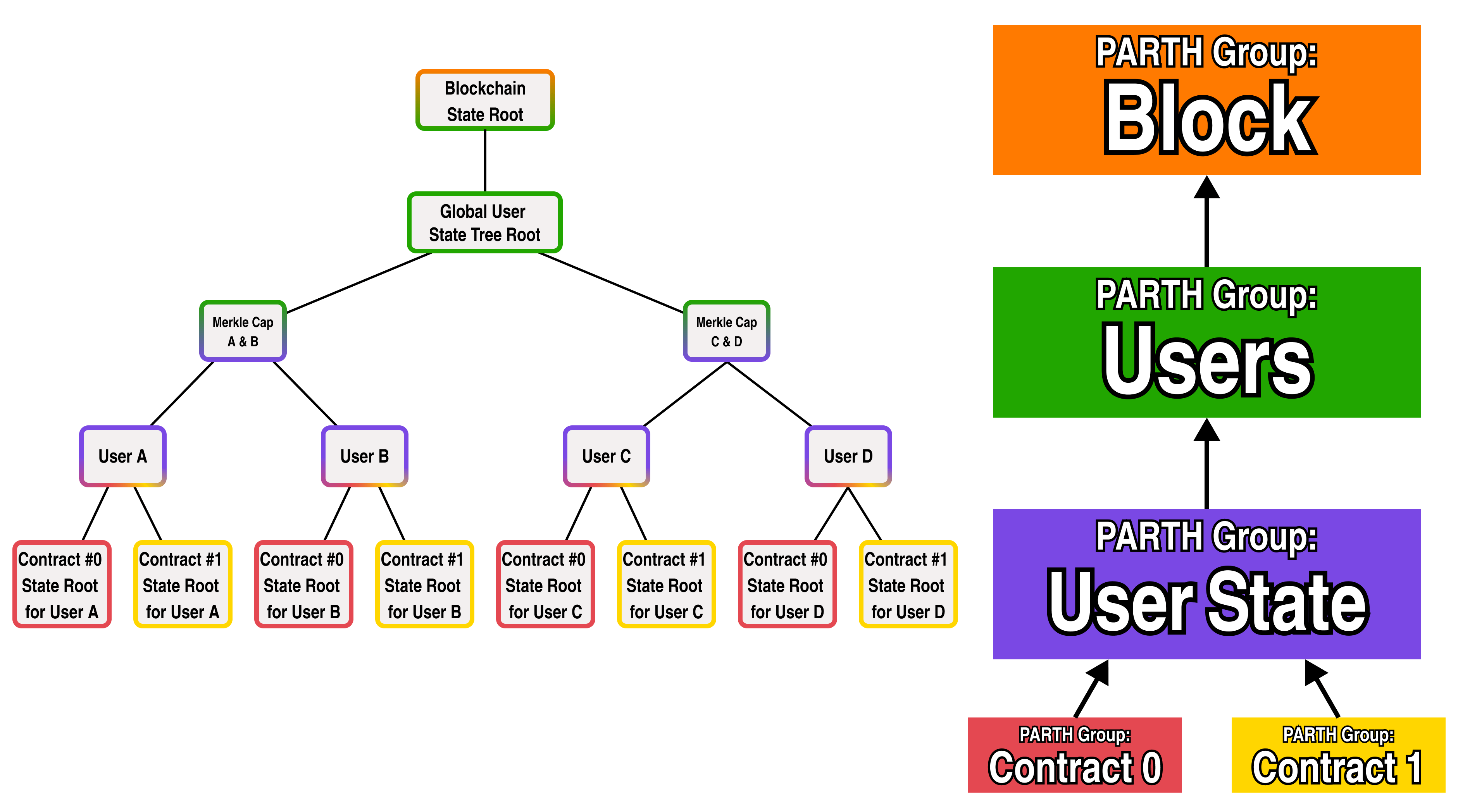
Great! We now have a complete representation for the contract state of a fully fledged blockchain, but we are missing a few critical state items from our tree, namely:
A place in the global state to store each public keys which identify each user
A place in the global state to store representations of smart contract logic
To tackle the problem of account abstraction, let's use zero knowledge proofs to act as a signature for users and represent a user's public key as the hash of the verifier data for their signature proof (for more details on this, you can check out the QED team's SDKEY paper).
For smart contract logic, we will represent each smart contract as a whitelist tree whose leaves are the hashes of each function in the smart contract's verifier data. In turn, we will add a global contract tree under the root blockchain tree whose leaves are the roots of each smart contract deployed to the blockchain.
Let's add the global contract tree and a public key under each user to our diagram:
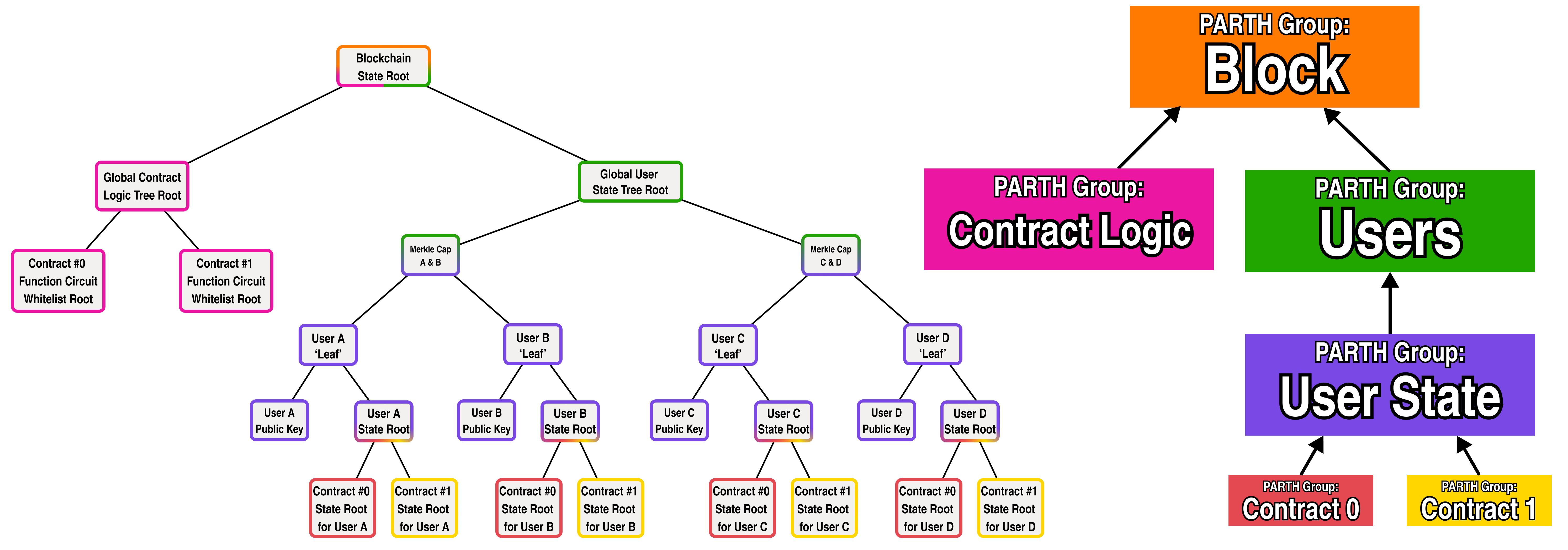
But hold on a second, you may be asking your self "what is this "verifier data" and how does it help us identify represent smart contracts or authenticate user signatures?"
Verifier Data
Since we will be talking a lot about proofs and "verifier data" as we continue, let's briefly discuss zero knowledge proofs (feel free to skip this section if you are ZK expert).
Note: Where ever possible, I will avoid discussing the sometimes complex mathematical underpinnings which underlies zero knowledge proof construction and instead prefer "blackbox" simplifications to lesson the burdon on the reader. While I will try to ensure that the analogies/simplifications I use to explain ZKP are both easy to understand and generally accurate, a full understanding of ZKP inevitably requires understanding the underlying math.
If, for example, I wanted to prove that 2+2 = 4 (proof A), 3+5=8 (proof B) and 2-2 = 0 (proof C), I would first generate two zero knowledge circuits by compiling "add2" and "subtract2", noting to return the inputs and result. The return result is known as the public inputs of the proof:
function add2(a: number, b: number) {
return [a, b, a + b];
}
function subtract2(a: number, b: number): number {
return [a, b, a - b];
}
When we execute one of our functions and generate a proof, the output will contain 3 key pieces of data:
The public inputs of our proof
- Think of "public inputs" as the data our ZK function returns
The verifier data of our function
- Think of "verifier data" as a special representation of our functions's logic that is unique to our function
The proof data
- Think of "proof data" as some special numbers that can be used in conjunction with our verifier data to show that it is possible to execute our ZK function and get the public inputs specified in our proof as the return result.
Once we compiled our functions I can generate proofs for A, B, and C, which would yield a result similar to the following:
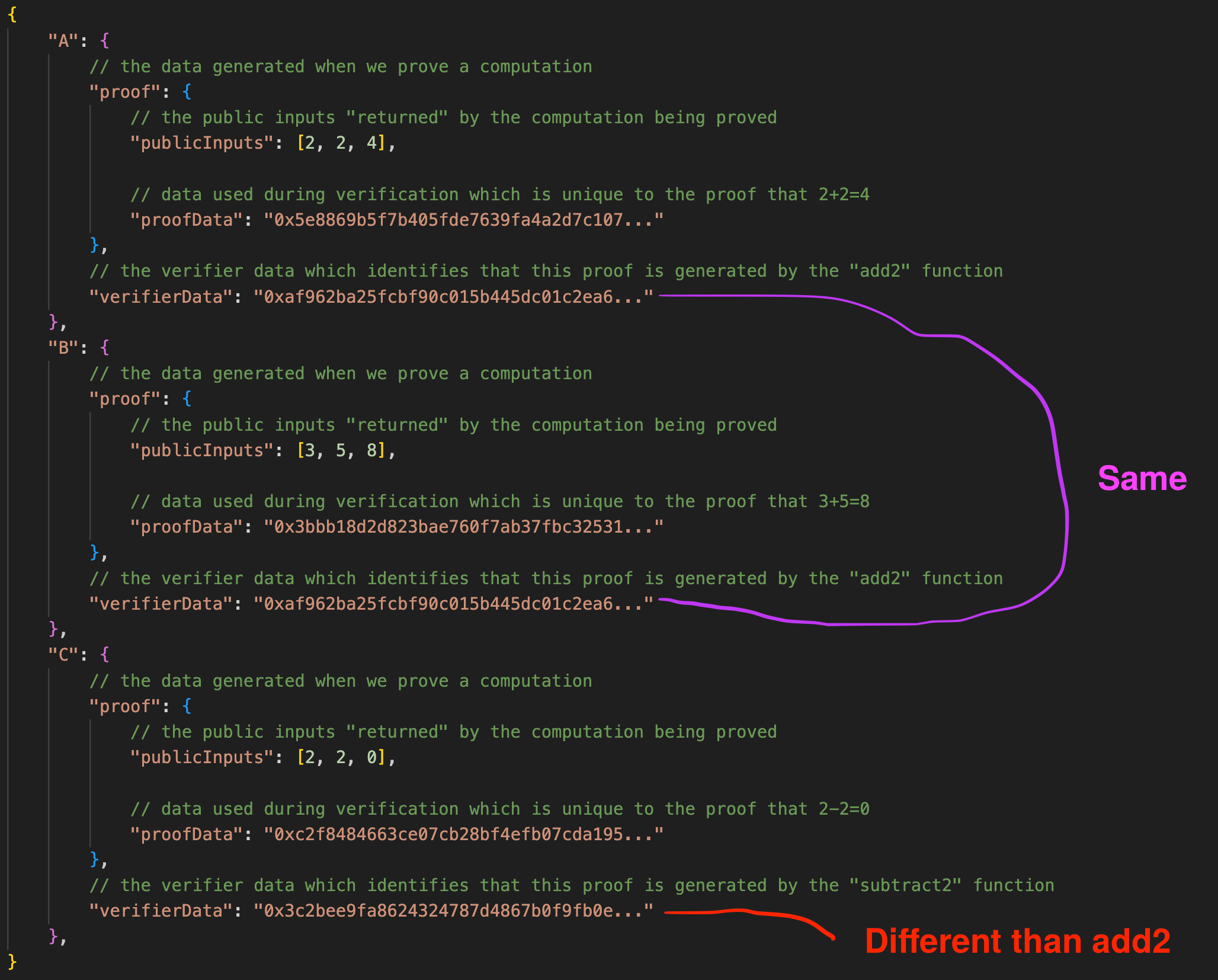
We can see that our proofs for 2+2=4 and 3+5=8 have the same verifier data, since the proof originated from the same function, add2. In addition, we can see that our proof for 2-2 has different verifier data than the addition proofs because the circuit logic is different. The neat thing is, for non-trivial functions, it turns out that it is possible to generate a proof for the function's return result which is faster to verify than just executing the function outright.
With this in mind, let's see how we can use zero knowledge proofs for user signatures and contract function calls on our blockchain.
ZK Signatures
On traditional blockchains (such as Ethereum and Bitcoin), users are represented by a point (an x and y value on a graph, also known as the user's public key), which is generated using a secret private key on a fancy mathematical construction known an elliptic curve. When users sign a transaction, they first hash the transaction and then apply a series of mathematical steps to generate a signature which can be checked to show that the signature was generated with the same private key used to generate the user's .
On our blockchain, we will represent a user's public key instead as a hash of the verifier data for a zero knowledge circuit that the user chooses. This gives us the flexibility to design custom signature logic, and also provides backwards compatibility with all existing blockchains.
To see how this is possible, let's make a signature circuit for one of our blockchain users which is compatible with their pre-existing Ethereum wallet. For this example, let's define the user's public key as a constant called .
const PUB_A: Point = {x: "0x...", y: "0x..."}; // The user's Ethereum Public Key
function userASignatureCircuit(hashToSign: Hash, ethSignature: Point){
const isSignatureValid: boolean = verifyEthSignature(PUB_A, hashToSign, ethSignature);
assert(isSignatureValid === true, "you must call the signature circuit with a valid signature");
return hashToSign;
}
In this case, the userASignatureCircuit function first verifies the Ethereum signature, constrains that the signature must be valid (if it is not valid for user A's public key, an error is thrown during proof generation), and then returns the hash to be signed as the public inputs of the proof.
If there exists a proof with userASignatureCircuit's verifier data and public inputs which correspond to some hash, then it proves that someone with the user's private key has signed the hash in the past and used the signature to generate the proof. If user A never signed the hash with their Ethereum private key, then it would likewise be impossible to generate a proof which is valid for userASignatureCircuit's verifier data!
Hence, verifying a proof generated by calling the ZK function userASignatureCircuit for some "hashToSign" is functionally equivalent to proving that user A has signed "hashToSign" with their Ethereum wallet!
ZK Smart Contract Functions
When a Smart Contract function is called by a blockchain transaction, it follows some predefined logic to modify the state of the contract. Looking at our previous diagram, we can see that each contract's state is represented by a state tree stored on chain for each user:
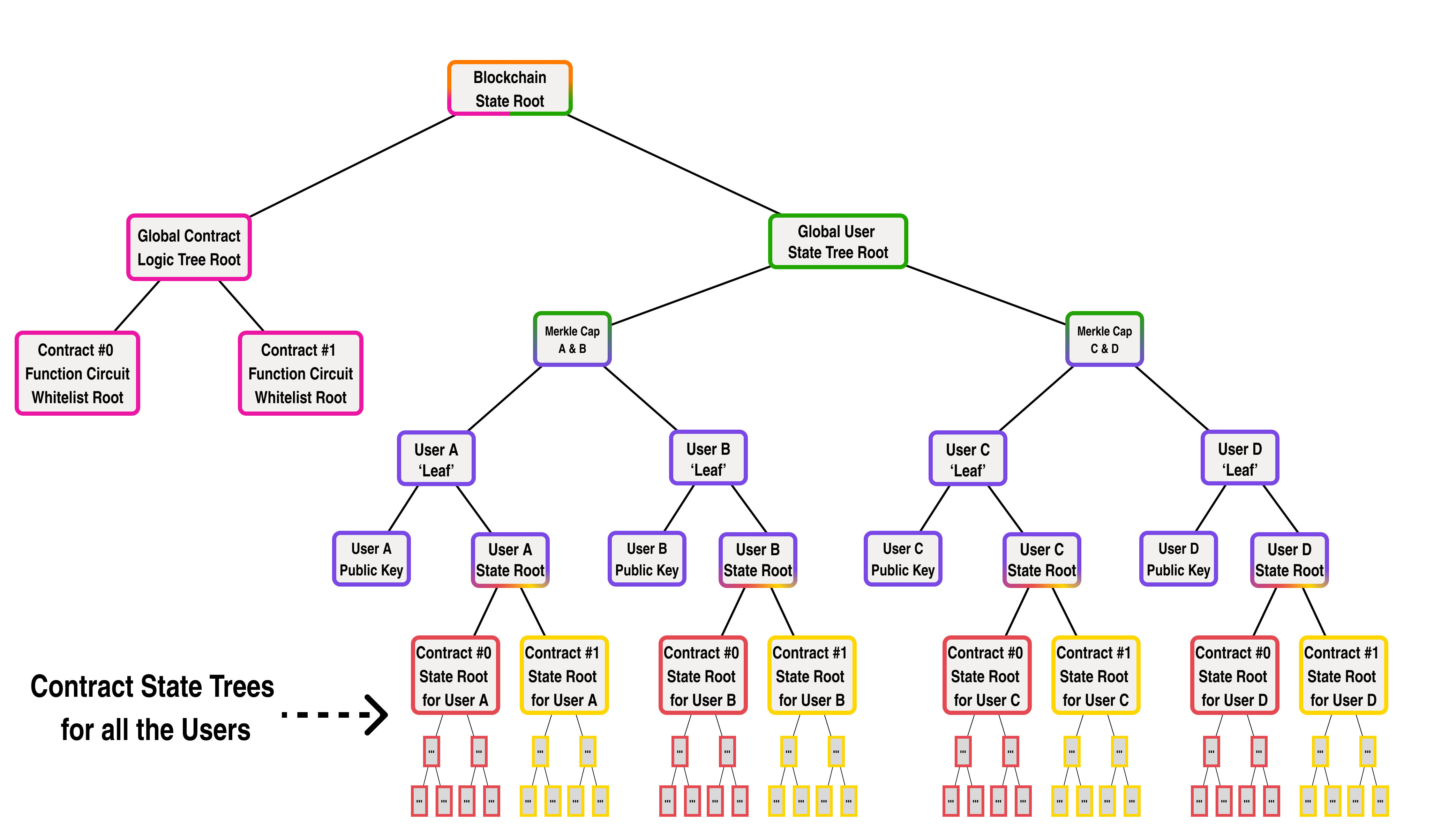
Since all a contract function does is perform a set of logical operations which update the contract's state root, we can represent a smart contract function as a ZK function which takes in the contract's current state root, performs some modifications and returns the new state root:
interface ContractExecutionContext {
// the root of the blockchain at the start of the current block
blockchainStateRoot: Hash;
// the user's current state root before running the transaciton
userStateRoot: Hash;
// the user's ID (the leaf index of the user's state tree)
userId: number;
// the contract's ID (the leaf index in the global contract tree)
contractId: number;
// the contract's state root before running the current transaction
contractStateRootBeforeTransaction: Hash;
}
interface ContractReturnResult {
context: ContractExecutionContext;
// the contract's state root after running the current transaction
contractStateRootAfterTransaction: Hash;
// a linear hash representing any external contract calls made by the contract function
// (you can ignore this for now)
externalCallProofDebt: Hash;
}
function exampleContractCall(context: ContractExecutionContext, arguments: any): ContractReturnResult {
let currentStateRoot = context.contractStateRootBeforeTransaction;
let currentExternalCallProofDebt = "0x00000000000000000000000000000000"; // ignore this for now
// do some computation, mutating the state root
// ...
// return the new state root and any external call proof debt
return {
context,
contractStateRootAfterTransaction: currentStateRoot,
externalCallProofDebt: currentExternalCallProofDebt,
};
}
Let's suppose that Contract #1 was a smart contract which stored the number of Diamonds and Rubies owned by each user for an on chain game. In addition to storing the number of diamonds and rubies held by each player, the contract also has a "buyRubies" function which allows the users to buy rubies using their diamonds at a price of 3 diamonds for 1 ruby.
In this scenario, the blockchain's state might look like the following:
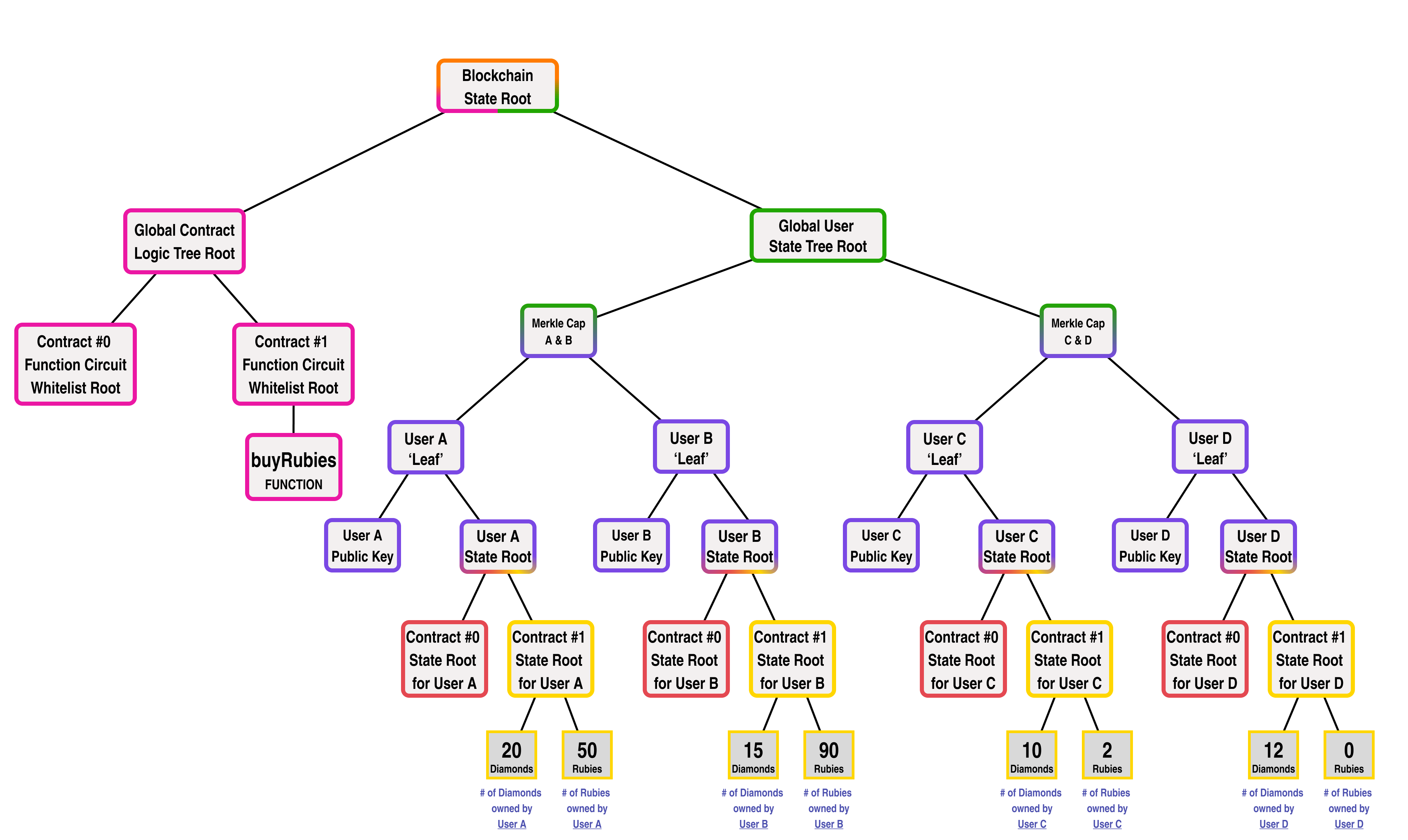
If we wanted to make a ZK circuit version of our buyRubies function, it could look like the following:
interface ContractExecutionContext {
// the root of the blockchain at the start of the current block
blockchainStateRoot: Hash;
// the user's current state root before running the transaciton
userStateRoot: Hash;
// the user's ID (the leaf index of the user's state tree)
userId: number;
// the contract's ID (the leaf index in the global contract tree)
contractId: number;
// the contract's state root before running the current transaction
contractStateRootBeforeTransaction: Hash;
}
interface ContractReturnResult {
context: ContractExecutionContext;
// the contract's state root after running the current transaction
contractStateRootAfterTransaction: Hash;
// a linear hash representing any external contract calls made by the contract function
// (you can ignore this for now)
externalCallProofDebt: Hash;
}
interface IDeltaMerkleProof {
// the leaf index of the tree
index: number;
// the siblings from the root of the tree to the leaf
siblings: Hash[];
// the old value of the state leaf before the modification
oldValue: BigNumber;
// the new value of the state leaf after the modification
newValue: BigNumber;
// the root of the tree before the modification
oldRoot: Hash;
// the root of the tree after the modification
newRoot: Hash;
}
interface IBuyRubiesArguments {
// the number of rubies to buy
numRubies: number;
updateDiamondsDMP: IDeltaMerkleProof;
updateRubiesDMP: IDeltaMerkleProof;
}
function buyRubies(context: ContractExecutionContext, args: IBuyRubiesArguments): ContractReturnResult {
let currentStateRoot = context.contractStateRootBeforeTransaction;
let currentExternalCallProofDebt = "0x00000000000000000000000000000000"; // ignore this for now
// the price of a ruby in diamonds
const price = 3;
const {updateDiamondsDMP, updateRubiesDMP, numRubies} = args;
// number of diamonds the user has to pay for the rubies
const totalCost = numRubies * price;
// verify the delta merkle proof which subtracts totalCost from the user's diamond balance
verifyDeltaMerkleProof(updateDiamondsDMP);
// ensure that the user is modifying their diamond balance
assert(updateDiamondsDMP.index === 0);
// ensure that the user is decrementing their diamond balance by 'totalCost'
assert(updateDiamondsDMP.oldValue - updateDiamondsDMP.newValue === totalCost);
// check for overflow
assert(updateDiamondsDMP.newValue < updateDiamondsDMP.oldValue);
// ensure that the user is starting their changes from the correct contract state root
assert(updateDiamondsDMP.oldRoot === currentStateRoot);
// update the current state root to the new state root after decrementing the user's diamond balance
currentStateRoot = updateDiamondsDMP.newRoot;
// verify the delta merkle proof which adds numRubies to the user's ruby balance
verifyDeltaMerkleProof(updateRubiesDMP);
// ensure that the user is modifying their ruby balance
assert(updateRubiesDMP.index === 1);
// ensure that the user is incrementing their ruby balance by 'numRubies'
assert(updateRubiesDMP.newValue - updateRubiesDMP.oldValue === numRubies);
// check for overflow
assert(updateRubiesDMP.newValue > updateRubiesDMP.oldValue);
// ensure that the user is starting their changes from the state root after decrementing the user's diamond balance
assert(updateRubiesDMP.oldRoot === currentStateRoot);
// update the current state root to the new state root after incrementing the user's ruby balance
currentStateRoot = updateRubiesDMP.newRoot;
// return the new state root and any external call proof debt
return {
context,
contractStateRootAfterTransaction: currentStateRoot,
externalCallProofDebt: currentExternalCallProofDebt,
};
}
If you are not familiar with Merkle Proofs or Delta Merkle Proofs, it is recommended to first read our Hacker's Guide to Merkle Trees which goes into detail on how they work.
Fortunately, QED has a contract compiler which takes care of this for us, allowing us to write the much similar code shown below:
Contract ABI:
#dapenversion 1.0.0
contract DiamondsAndRubiesExampleContract {
var rubyBalance biguint;
var diamondBalance biguint;
fn buyRubies(numRubies: biguint);
}
Contract:
class DiamondsAndRubiesContractImplementation extends DiamondsAndRubiesContractContractBase{
buyRubies({numRubies}: {numRubies: biguint}){
const price = 3;
const totalCost = numRubies*price;
assert(this.state.diamondBalance >= totalCost, "you do not have enough diamonds");
this.state.diamondBalance -= totalCost;
this.state.rubyBalance += numRubies;
}
}
When a smart contract is called, therefore, we generate a proof that the contract called by the transaction's state tree has legally update from its previous root value to a new root value.
Putting it all together
Now that we have a means for storing the user's public key and contract functions, we can figure out a process by which users could submit transactions to our blockchain.
If we want to prove the result of several transactions for a given user, we could use the following process which we call the "User Proving Session" or UPS:
Start UPS Session: Generate a proof which shows that a given user with ID exists in a blockchain with root at a certain block , and the the user has start state and current state root
Prove Contract Transaction: Generate a proof of a transaction which modifies the state tree of contract id
UPS Transact: Generate a proof which recursively verifies the transaction proof generated in step 2 and the previous UPS proof (if it is the first transaction, verify the Start UPS Session proof, otherwise verify the last UPS Transact proof), and update the user's state root with a delta merkle proof which connects the end state root of the previous UPS proof to the start of the delta merkle proof, and the value to the new and old roots in the public inputs of the contract transaction proof. Update to equal the new user state root.
Repeat steps 2-3 for all the transactions the user would like to execute
Signature: Generate a signature proof which signs hash(userId + nonce + start state root + end state root)
End Cap: Generate an end cap proof which recursively verifies the last UPS proof and the signature proof, ensuring that the payload hash of the signature corresponds to the state root transition from to
After generating the end cap proof, the user can send the End Cap proof along with their state deltas to the decentralized proving network generate a final block proof in parallel.
Let's update our flow diagram to reflect our new block proof creation process:
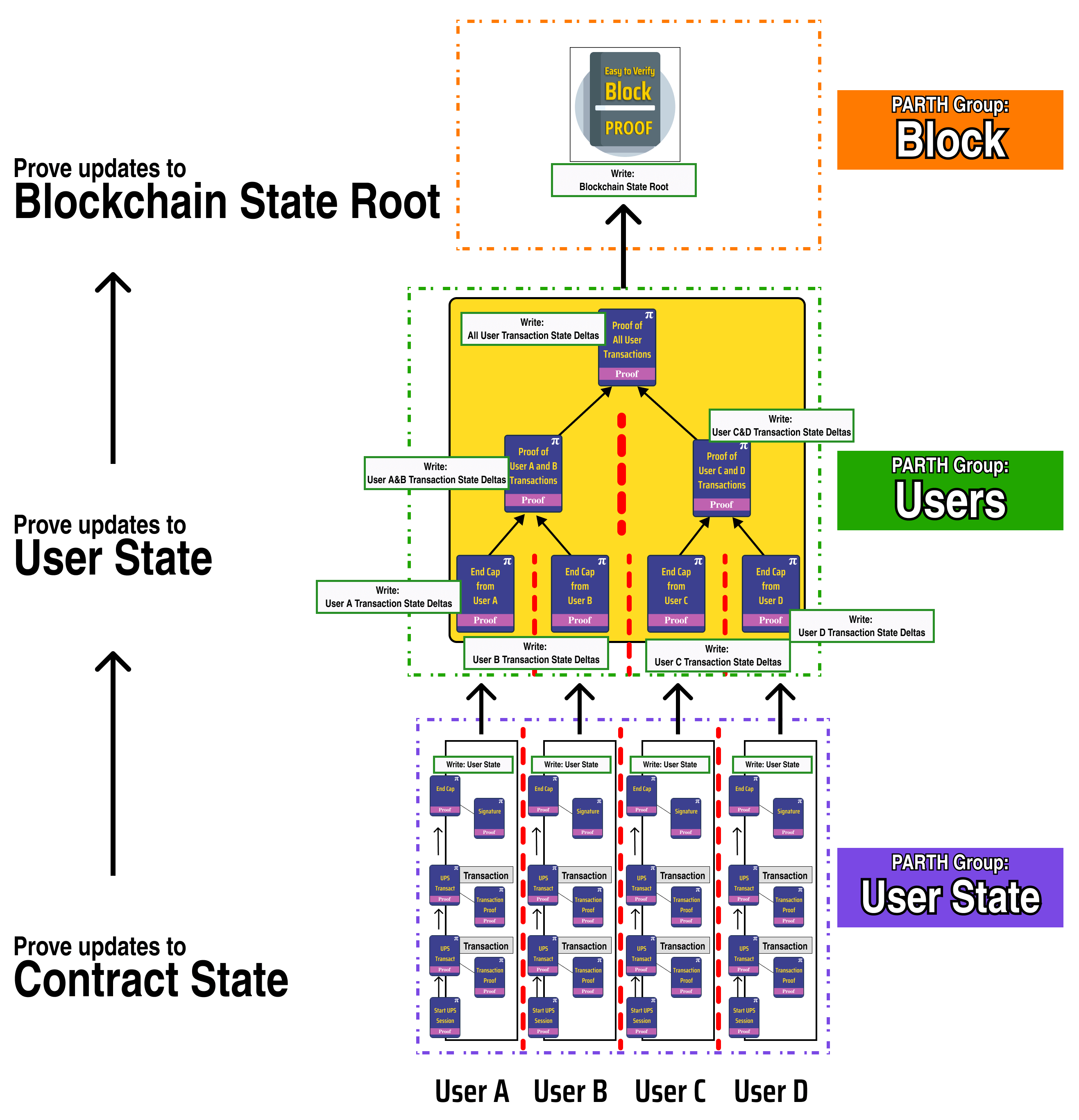
If we consider our previous contract example with rubies and diamonds, let's see what this looks like with our new User Proving Session.
In our previous example, the users started with the following balances:
| User | # of Diamonds | # of Rubies |
|---|---|---|
| Alice (User A) | 20 | 50 |
| Bob (User B) | 15 | 90 |
| Carol (User C) | 10 | 2 |
| Mike (User D) | 12 | 0 |
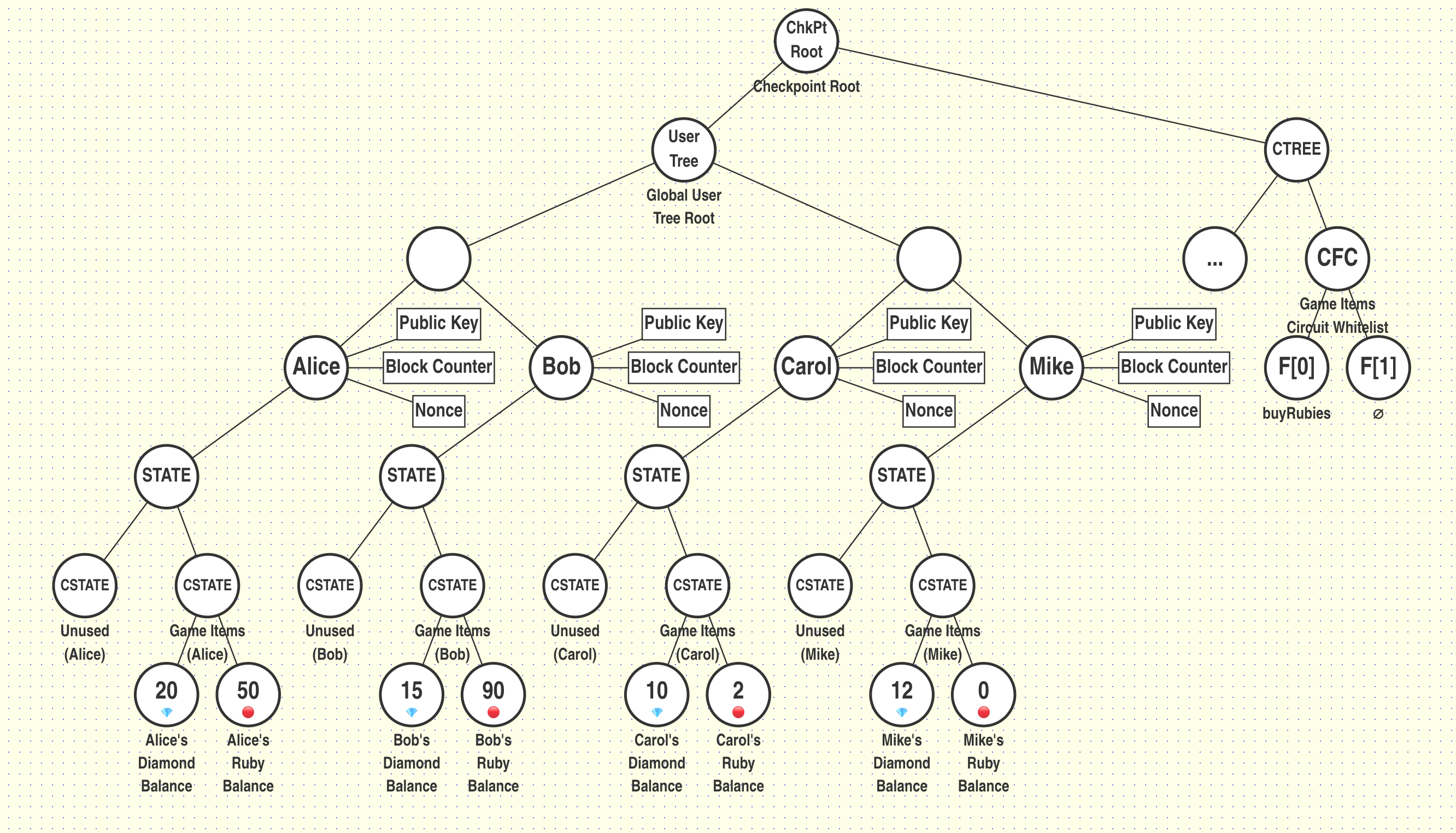
In the next block, let's suppose the following transactions occur:
Alice buys 3 rubies for 9 diamonds
Bob buys 2 rubies for 6 diamonds
Carol buys 3 rubies for 9 diamonds
Mike buys 4 rubies for 12 diamonds
To help us better understand how the User Proving Session works, lets examine how each step works in the animation of Alice's UPS below:
Note how all of Alice's writes are isolated to her own tree, and how the only data she reads outside of her tree is the state of the blockchain as it was at the end of the last block. This means we can allow Alice to prove her transactions and user proving session locally, meaning the only work that needs to be done by the network is the tree aggregation of the user's proofs and storing the state deltas!
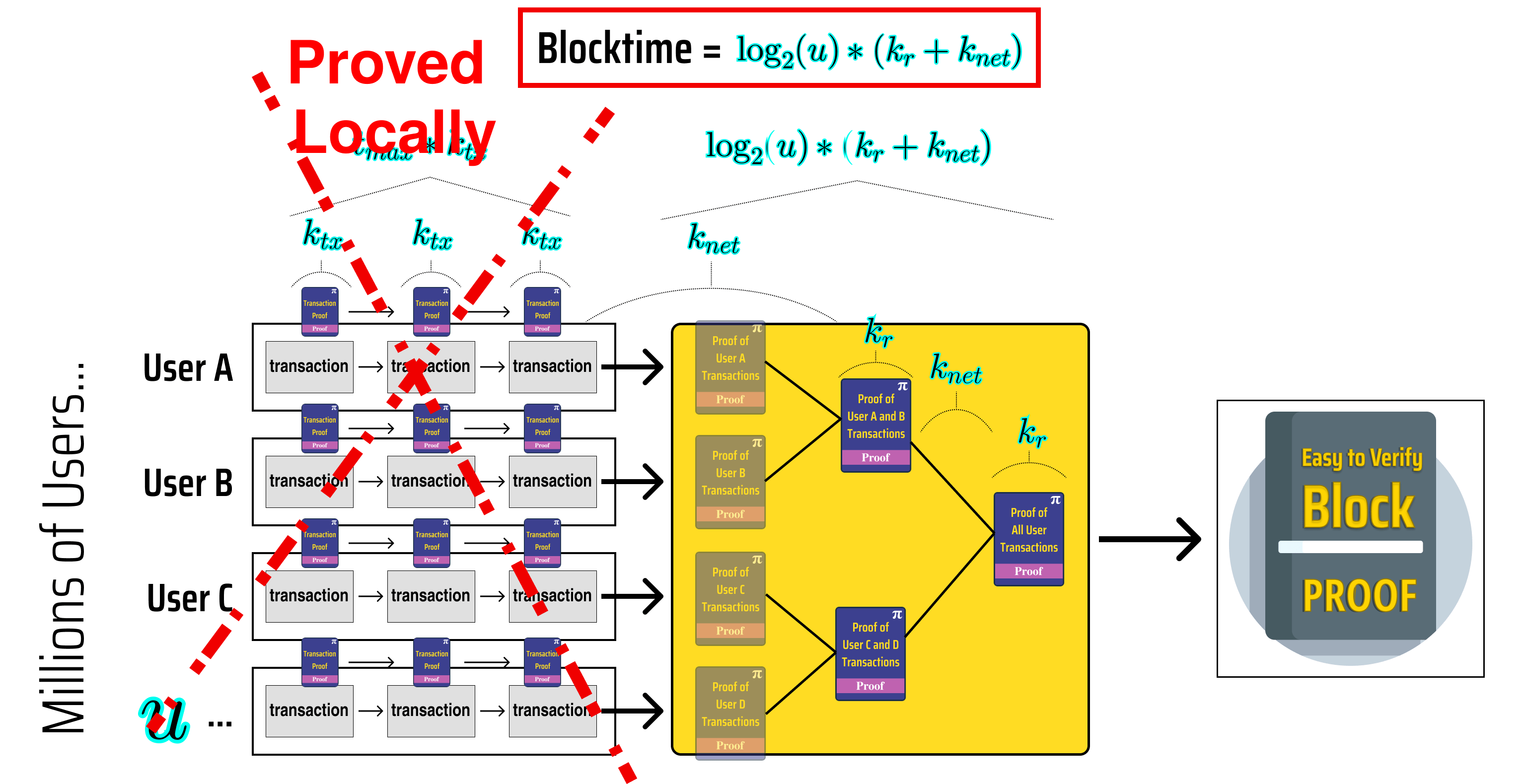
Our block time is now:
...and no longer depends on the number of transactions made by each user 🎉!
Let's see what the whole block looks like just to make sure our new architecture works properly:
As we can see the only work that needs to be done by the blockchain network are the final steps:
Confirming that our blockchain's block time is 🎉!
Looks good so far! But a blockchain would not be complete without support for 3rd party tokens. In the next section, let's see how we can implement a USDT token and see our architectures horizontal scalability start to really shine.
Token Example
On traditional blockchains, we would store the token balances of the users a mapping of user id to balance, but that is not going to work on our architecture due to our hard guarantees against race conditions.
Instead, for each user, let's store the users balance, the total amount sent by the user to every other user and the total amount received from each user (thanks to Zero Merkle Trees, our blockchain nodes will only have to store the non-zero balances).
Our token's Dapen ABI definition will look like the following:
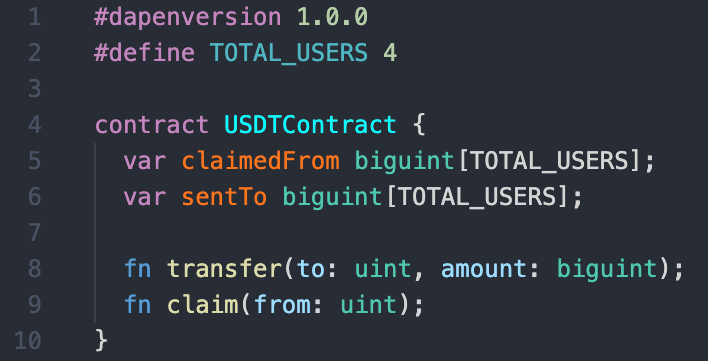
Since there isn't much of a meaning to saying how much a user has claimed from or sent to themselves, we will let claimedFrom[<a user's own id>] represent their balance and sentTo[<a user's own id>] represent null (unused value).
And for our contract code we can use the following:
class USDTContractImplementation extends USDTContractContractBase{
transfer({to, amount}: IDPNGenUSDTContractFunctionArgsTransfer): void{
assert(to !== this.userId, "you cannot send tokens to yourself");
// we need to have a balance >= the amount we want to sent
assert(this.state.claimedFrom[this.userId] >= amount, "insufficient balance");
// decrement our balance by amount
this.state.claimedFrom[this.userId] -= amount;
// increment the sent amount to `to` by the amount of tokens we want to send
this.state.sentTo[to] += amount;
}
claim({from}: IDPNGenUSDTContractFunctionArgsClaimTransfer): void{
assert(from !== this.userId, "you cannot claim tokens from yourself");
// contractFor obtains a read only instance of the contract for another user
const totalSentFromOtherUser = this.contractFor(from).state.sentTo[this.userId];
// the number of tokens we have previously claimed from the other user
const totalClaimedFromOtherUser = this.state.claimedFrom[from];
// ensure there are outstanding tokens to claim
assert(totalSentFromOtherUser>totalClaimedFromOtherUser, "no tokens to claim");
// the amount of tokens we haven't claimed yet
const claimAmount = totalSentFromOtherUser-totalClaimedFromOtherUser;
// set the amount claimed to the total sent from the other user
this.state.claimedFrom[from]=totalSentFromOtherUser;
// add claimAmount to our balance
this.state.claimedFrom[this.userId]+=claimAmount;
}
}
Let's see what the start state of this token contract looks like with the following initial balances:
| User | Balance (USDT) |
|---|---|
| Alice | 300 USDT |
| Bob | 100 USDT |
| Carol | 500 USDT |
| Mike | 90 USDT |
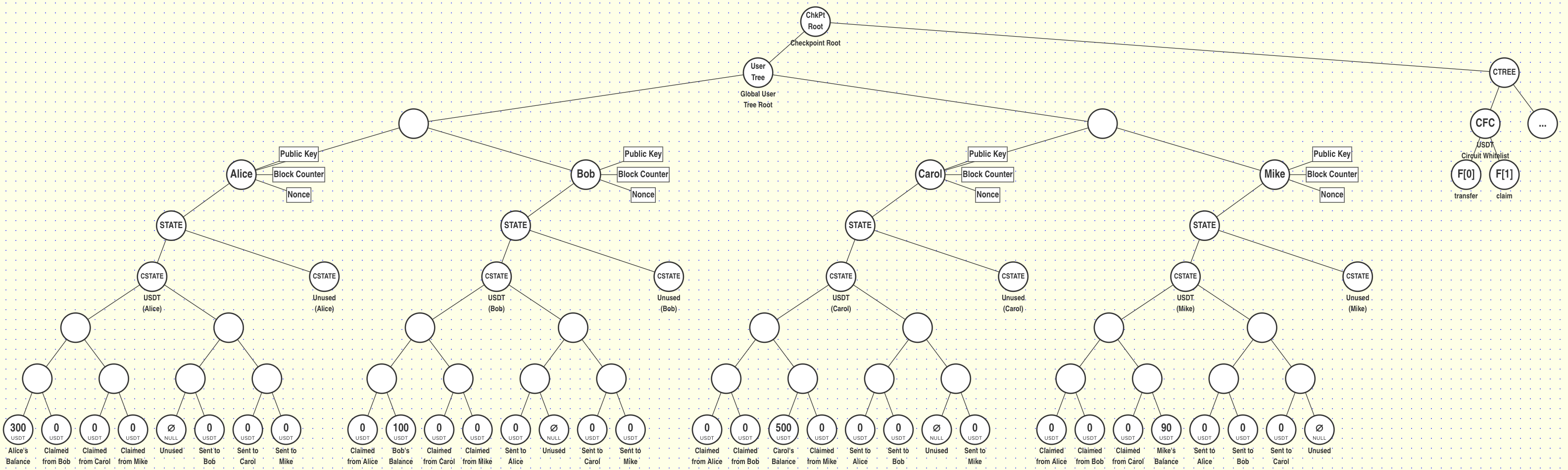
Let's visualize a scenario where the following transactions occur:
Block #1:
Alice sends 30 USDT to Bob
Bob sends 50 USDT to Carol
Carol sends 40 USDT to Mike
Mike Sends 20 USDT to Bob
Block #2:
Bob claims the USDT sent from Alice and Mike
Carol claims the USDT sent from Bob
Mike claims the USDT sent from Carol
Like before, let's first zoom in and see what Alice's local proving session looks like:
We can see that Alice transferred 30 USDT to Bob by calling the transfer function on the contract, which decremented her own balance by 30 USDT and incremented the amount she has sent to Bob by 30 USDT.
In the next block, Bob can then claim the tokens from Alice by proving that the amount he has claimed from Alice in the past (0 USDT) is less than the amount Alice has sent to him (he can claim the difference of 30-0 = 30 USDT).
Let's now zoom out and see all of our transactions vizualized:
Like the first example with our gems the only work that needed to be completed by the network was the final aggregation step at the end (all of the bottom proving is done locally by the users themselves!). This also shows that our architecture's ability to scale does not depend on the kinds of transactions executed in the block, the primarily failing of previous "scalable" blockchains which claimed 100,000+ TPS!
Closing Thoughts
Congratulations on joining along in our journey to design a horizontally scalable blockchain. Scalability is not just a marketing term to boost token prices, it is a reflection of how many people can make use of a technology, and a ceiling of how impactful a technology can be on the rest of society. As we spend more and more of our lives on the internet, it is becoming increasingly clear that our digital society must transition important virtual interactions to a trustless, provably fair playing field, lest we find ourselves living our lives at in digital dictatorship of mega platforms and at the mercy of the whims of executives at Twitter, Facebook and Google. Using the techniques described in this post, we hope that ZK (and our protocol, QED) can help bring about a fairer internet, and encourage others to explore how to improve scalability of trustless systems across the board.
Many of the techniques (+more) discussed in this post were used to design QED's blockchain architecture. In future posts, we will discuss covenants (used for multi-user interactions/transactions), how to build an on chain DEX on QED and provide smart contract quick starts for those looking to build on QED.
To stay up to date with the latest news from QED, follow our socials or check back on the QED blog for the latest posts: